RBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability

These comprehensive RBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 5 Notes Continuity and Differentiability

Introduction:
In previous class, we had learnt to differentiate certain functions like polynomial functions and trigonometric functions. In this chapter, we will study continuity, differentiability and relations between them along with some other functions like inverse trigonemetric function, exponential and logarithmic functions. We will learn some fundamental theorems in this area.

If we sketch a graph of a function y = f(x) and at any point x = a this graph has no break or jump, then function is said to be continuous at that point otherwise discontinuous.

Example:

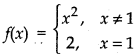
Following is the sketch of function f(x)
From graph, it is clear that at x = 1 graph breaks. Thus function is discontinuous at x = 1 and is continuous at other points.


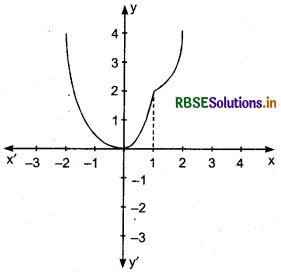
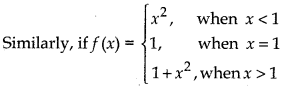
Graph of this function is shown in the following figure:
From figure, it is clear that, at x = 1 graph breaks. Thus at x = 1, function is discontinuous.

Since, it is difficult to draw graph of all the functions, so mathematically, continuity is defined on the basis of limit.

 

Continuity of A Function
Definition 1: Suppose/is a real function on a subset of the real numbers and let c be a point in the domain of f.
Then f is continuous at c if
\(\lim _{x \rightarrow c}\) f(x) = f(c)
More elaborately, if the left hand limit, right hand limit and the value of the function at x = c exist and equal to each other, then/is said to be continuous at x = c. Recall that if the right hand and left hand limits at x c coincide, then we say that the common value is the limit of the function at x = c. Hence, we may also rephrase the definition of continuity as follows : a function is continuous at x = c if the function is defined at x = c and if the value of the function at x = c equals the limit of the function at x = c. If f is not continuous at c, we say/is discontinuous at c and c is called a point of discontinuity of f.

Definition 2: A real function f is said to be continuous if it is continuous at every point in the domain of f.
Suppose f is a function defined on a closed interval [a, b], then for f to be continuous, it needs to be continuous at every point in [a, b] including the end point a and b. Continuity of /at a means
\(\lim _{x \rightarrow a^{+}}\) f(x) = f(a)
and continuity of/at b means
\(\lim _{x \rightarrow b^{-}}\) f(x) = f(b)

Observe that \(\lim _{x \rightarrow \bar{a}}\) f(x) and \(\lim _{x \rightarrow \bar{b}}\) do not make sense.
As a consequence of this definition, if f is defined only at one point, it is continuous there, i.e., if the domain of f is singleton, f is a continuous function.

Algebra of Continuous Functions:
In the previous class, after having understood the concept of limits, we learnt some algebra of limits. Analogously, now we will study some algebra of continuous functions. Since, continuity of a function at a point is entirely dictated by the limit of the function at that point, it is reasonable to expect result analogous to the case of limits.

Theorem 1.
Suppose f and g be two real functions continuous at a real number a, then
(i) f + g is continuous at x = a.
(ii) f - g is continuous at x = a:
(iii) Product of any constants and function is continuous at x = a.
(iv) f. g is continuous at x - a.
(v) \(\left(\frac{f}{g}\right)\) is continuous at x = a (provided g(a) ≠ 0).
(vi) Inverse of function \(\frac{1}{f(x)}\) is continuous at point x = a whereas f(a) ≠ 0.
Proof :
We are investigating continuity of (f + g) at x = a. Clearly it is defined at x = a. We have
(i) f + g is continuous at x = a.

Thus, f + g is continuous at x = a.

(ii) f - g is continuous at x = a:

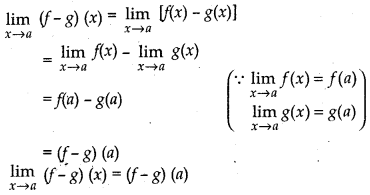
Thus, f - g is continuous at x = a.

(iii) Product of any constants and function is continuous at x = a.

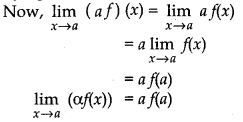
Thus, af(x) is continuous at x = a.

(iv) f. g is continuous at x - a.

Thus, fg is continuous at x - a

(v) \(\left(\frac{f}{g}\right)\) is continuous at x = a (provided g(a) ≠ 0).

Thus, \(\frac{f}{g}\) is continuous at x = a (∵ g(a) ≠ 0)

(vi) Inverse of function \(\frac{1}{f(x)}\) is continuous at point x = a whereas f(a) ≠ 0.

Thus, inverse of f, i.e \(\frac{1}{f(x)}\) is a continuous at x = a

Remarks:
1. As a special case of (iv) above, if/is a constant function, i.e., f(x) = λ for some real number λ, then the function (λ.g) defined by (λ.g)(x) = λ.g(x) is also continuous. In particular, if λ = - 1, the continuity off implies continuity of -f.

2. As a special case of (v) above, iff is the constant function f(x) = λ, then the function \(\frac{\lambda}{g}\) defined by \(\frac{\lambda}{g}(x)=\frac{\lambda}{g(x)}\) is also continuous wherever g(x) ≠ 0. In particular, the continuity of g implies continuity of \(\frac{1}{g(x)}\)

Theorem 2.
Let f and g be real functions such that fog is defined. If g is continuous at x = a and f is continuous at g(a), show that fog is continuous at x = a.
Proof:
Since, fog is defined. Therefore Range (g) ∈ Domain (f)
⇒ g(x) ∈ domain (f) for all
x ∈ domain (g)
Now, g(x) is continuous at x = a.

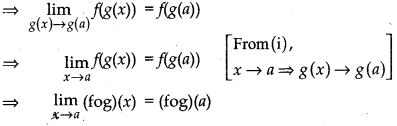
⇒ fog is continuous at x = a.

Differentiability of A Function
Let f(x) be a real valued function defined by an open interval (a, b) and let c ∈ (a, b). Then f(x) is said to be differentiable or derivable at x = c, if \(\lim _{x \rightarrow c^{+}} \frac{f(x)-f(c)}{x-c}\) exists finitely.

This limit is called the derivative or differential coefficient of the function/(x) at x = c and is denoted by

is called the right hand derivative of f (x) at x = c and is denoted by f'(c⁺) or Rf‘(c).
Thus, f is differentiable at x = c.
⇔ Lf'(c) = Rf'(c)
If Lf (c) = Rf (c), we say that f(x) is not differentiable at x = c.

Theorem :
If a function is differentiable at a point, it is necessarily continuous at that point. But, the converse is not necessarily true.
OR
f(x) is differentiable at x = c.
⇒ f(x) is continuous at x = c.
Proof:
Let a function f(x) be differentiable at x = c.
Then, \(\lim _{x \rightarrow c^{+}} \frac{f(x)-f(c)}{x-c}\) exists finitely.
Let, \(\lim _{x \rightarrow c^{+}} \frac{f(x)-f(c)}{x-c}\) = f'(c) ..........(1)

In order to prove that f(x) is continuous at x = c, it is sufficient to show
\(\lim _{x \rightarrow c^{+}}\) f(x) = f(c).
Now,

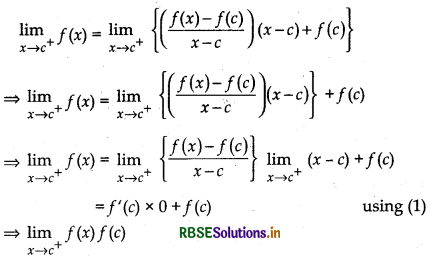
Note :
Converse of this theorem is not true.
For example, we have seen the function defined by f(x) = |x| is a continuous function. Consider the left hand limit.
\(\lim _{h \rightarrow 0^{-}} \frac{f(0+h)-f(0)}{h}=\frac{-h}{h}\) = -1
The right hand limit
\(\lim _{h \rightarrow 0^{+}} \frac{f(0+h)-f(0)}{h}=\frac{h}{h}\) = 1
Since, the above left and right hand limits at x = 0 are not equal, therefore, \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}\) does not exist and hence f is not differentiable at x = 0.

Differentiation :
Suppose f is real function and c is a point in its domain. The derivative of f at c is defined by
\(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\)
provided this limit exists. Derivative of/at c is denoted by f'(c) or \(\frac{d}{d x} (f(x))\). The function is defined by
f'(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

Wherever the limit exists is defined to be the derivative of f. The derivative of f is denoted by f' (x) or \(\frac{d}{d x}\) (f(x)) or if y = f(x) by \(\frac{dy}{d x}\) or y'. The process of finding derivative of a function is called differentiation. We also use the phrase differentiate f(x) with respect to x to mean function f'(x).

The following rules were established as a part of algebra of derivatives:

• (1) (u ± v)' = u' ± v'
• (2) (uv)' = u'v + uv' (Leibniz or product rule)
• (3) \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}\), wherever v ≠ 0 (Quotient rule)

Whenever we defined derivative, we has put a caution provided the limit exists. Now the natural question is; what if it doesn't? The question is quite pertinent and so is its answer. If \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) does not exist, we say that f is not differentiable at c. In other words, we say that a function f is differentiable at a point c in its domain if both \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) and \(\lim _{h \rightarrow 0^{+}} \frac{f(c+h)-f(c)}{h}\) are finite and equal. A function is said to be differentiable in an interval [a, b] if it is differentiable at every point of [a, b]. As in case of continuity, at the end point a and b, we take the right hand limit and left hand limit, which are nothing but left hand derivative and right hand derivative of the function at a and b respectively. Similarly, a function is said to be differentiable in an interval (a, b) if it is differentiable at every point of (a, b).

Derivative of Composite Functions
To study derivative of composite function we start with an illustrative example. Say, we want to find the derivative of/, where
f(x) = (2x + 1)³
One way is to expand (2x +1)³ using binomial theorem and find the derivative as a polynomial function as illustrated below.
\(\frac{d}{d x}\)f(x) = \(\frac{d}{d x}\)[(2x+1)³]
= \(\frac{d}{d x}\)(8x³ +12x² + 6x +1)
= 24x² + 24x + 6
= 6 (2x + 1)²

Now, observe that
f(x) = (fog)(x)
Where g(x) = 2x + 1 and h(x) = x³. Put f = g(x) = 2x + 1.
Then/(x) = h(t) = t³. Thus \(\frac{d f}{d x}\) = 6 (2x + 1)² = 3(2x + 1)².
2 = 3t². 2 = \(\frac{d h}{d t} \cdot \frac{d t}{d x}\)
The advantage with such observation is that it simplifies the calculation in finding the derivative of, say, (2x + 1)¹⁰⁰. We may formalise this observation in the following theorem called the chain rule.
Theorem (Chain Rule) Let/be a real valued function which is a composite of two function u and v; i.e.,f = v o u,
Suppose t = u(x) and if both \(\frac{d t}{d x}\) and \(\frac{d v}{d t}\) exist, we have
\(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)
We skip the proof of this theorem. Chain rule may be extended as follows. Suppose f is a real valued function which is a composite of three function u, v and w; i.e.,
f = (w o u) o v
If t = v (x) and s = u (t), then
\(\frac{d f}{d x}=\frac{d(w o u)}{d t} \cdot \frac{d t}{d x}\)
= \(\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x}\)
provided all the derivatives in the statement exist. Reader is invited to formulate chain rule for composite of more functions.

Derivatives of Implicit Functions
Untill now we have discussed derivatives of functions of the form y = f(x). If the variables x and y are connected by a relation of the form f(x, y) = 0 and it is not possible or convenient to express y as a function in the form y = 0(x), then y is said to be an implicit function of x. To find \(\frac{d y}{d x}\) in such a case, we differentiate both sides of the given relation with respect to x.
Example: y + cos y = sin x is an implicit functions.

Derivatives of Inverse Trigonometric Functions
In this section we will find the derivatives of inverse functions from first principle or by delta method.
Following results will be very useful to find the same.

• sin^-1 x + sin^-1y = sin^-1 (x\(\sqrt{1-y^{2}}\) + y\(\sqrt{1-x^{2}}\))
• sin^-1 x - sin^-1 y = sin^-1 (x\(\sqrt{1-y^{2}}\) - y\(\sqrt{1-x^{2}}\))
• cos^-1 x + cos^-1 y = cos^-1(xy - \(\sqrt{1-x^{2}} \sqrt{1-y^{2}}\))
• cos^-1x - cos^-1 y = cos^-1 (xy + \(\sqrt{1-x^{2}} \sqrt{1-y^{2}}\))
• tan^-1 x + tan^-1 y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)
• tan^-1 x - tan^-1 y = tan^-1\(\left(\frac{x-y}{1+x y}\right)\)
• \(\left(\frac{x+y}{1-x y}\right)\) = 1
• \(\lim _{x \rightarrow 0} \frac{\tan ^{-1} x}{x}\) = 1

Domain and range of inverse trigonometrical functions

• sin^-1x ⇒ Domain is [-1,1] and range is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
• cos^-1x ⇒ Domain [-1,1] and range is [0, π]
• tan^-1x ⇒ Domain and range is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
• cot^-1x ⇒ Domain and range is (0, π)
• sec^-1x ⇒ Domain is R - (- 1, 1) and range is [0, π] - [π/2]
• cosec^-1x ⇒ Domain R - (- 1, 1) and range is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) - {0}

Theorem 1 :
Differentiate function sin^-1x by first principle when x e (-1,1) and show that
\(\frac{d}{d x}\)sin^-1x = \(\frac{1}{\sqrt{1-x^{2}}}\)
Proof:
Let fix) = sin^-1x, then
f(x + h) = sin^-1(x + h)

Multiplying numerator and denominetor by

Alternatively:
Let sin^-1 = y
x = sin y

Theorem 2.
Differentiate cos^-1x by first principle and prove that
\(\frac{d}{d x}\)(cos^-1x) = -\(\frac{1}{\sqrt{1-x^{2}}}\) -1 < x < 1
Proof:
Let f(x) = cos^-1x, then
f(x + h) = cos^-1(x + h)

Theorem 3.
Differentiate tan^-1x by first principle and prove that
\(\frac{d}{d x}\) (tan^-1x) = \(\frac{1}{1+x^{2}}\)
Proof:
Let f(x) = tan^-1x
then f(x + h) = tan^-1(x + h)

Theorem 4.
Differentiate cot^-1x by first principle and show that
\(\frac{d}{d x}\)(cot^-1x) = -\(\frac{1}{1+x^{2}}\)
Proof:
Let f(x) = cot^-1x then
f(x + h) = cot^-1(x + h)

Theorem 5:
Differentiate sec^-1x by first principle and show that
\(\frac{d}{d x}\)sec^-1x = \(\frac{1}{|x| \sqrt{x^{2}-1}}\) where x ∈ R - [-1, 1]
Proof:
Let f(x) = sec^-1x

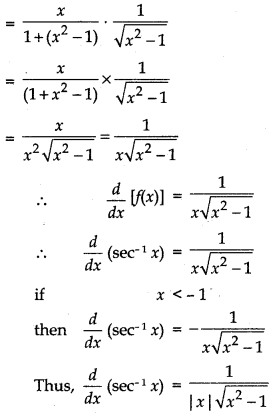
Theorem 6 :
Differentiate cosec^-1x by first principle and show that
\(\frac{d}{d x}\)cosec^-1x = -\(\frac{1}{|x| \sqrt{x^{2}-1}}\) where x ∈ R - [-1, 1]
Proof:
Let f(x) = cosec^-1x
then f(x + h) = cosec^-1(x + h)

Following are the formulae for derivative of inverse trigonometric functions:

• \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\)
• \(\frac{d}{d x}\)(cos^-1x) = -\(\frac{1}{\sqrt{1-x^{2}}}\)
• \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^{2}}\)
• \(\frac{d}{d x}\)cot^-1x = -\(\frac{1}{1+x^{2}}\)
• \(\frac{d}{d x}\)sec^-1x = \(\frac{1}{|x| \sqrt{x^{2}-1}}\)
• \(\frac{d}{d x}\)cosec^-1x = -\(\frac{1}{|x| \sqrt{x^{2}-1}}\)

Differentiationof a function of a function
In this section, we will study about the differentiation of composition of two or more functions by chain rule.
Chain Rule : If z = f(y) and y = g (x)
then \(\frac{d z}{d x}=\frac{d z}{d y} \cdot \frac{d y}{d x}\)
This rule can be extended further.

Exponential And Logarithmic Functions
Exponential function : If a is any real number such that f (x) = ax, where a > 0, a ≠ 1 then function f(x) = a^x is called exponential function whose domain is set of all real numbers and range is set of positive real numbers, i.e.,
Domain = R (set of real numbers)
Range = R+ (set of positive real numbers)
When a = e
Then, functionf(x) = a^x
⇒ f(x) = e^x
This function is called natural exponential function.
Therefore, f(x)= e^x (natural exponential function)

Logarithm of b on base a is symbolically written as
log a^b = x
If a = 10, i.e., base is 10 then log₁₀x is called common logarithm and if base is e, then we say that it is natural logarithm.
Thus, f(x)= log_ex or log x which is natural logarithm. For logarithm, following formula can be verified :

• log (xy) = logx + logy
• log \(\left(\frac{x}{y}\right) \)= logx- logy
• log (xⁿ) = n log x
• log_ax × log_x a = 1 [or log_ax = \(\frac{1}{\log _{x} a}\)]
• log_e e = 1 and log_e1 = 0

Derivatives of Exponential and Logarithmic Function:

• \(\frac{d}{d x}\)(e^x) = e^x
• \(\frac{d}{d x}\)(log_ex) = \(\frac{1}{x}\)

Logarithmic Differentiation
In this section, we will learn to differentiate certain special class of function given in the form :
y = f(x) = [u(x)]^v(x)
By taking log of both sides, we get
log y = v (x) log [u(x)]

Differentiating using chain rule
\(\frac{1}{y} \frac{d y}{d x}=\frac{v(x) \cdot 1}{u(x)}\). u'(x) + v'(x).log[u(x)]
⇒ \(\frac{d y}{d x}\) = [\(\frac{v(x)}{u(x)}\)u'(x) + v'(x).log[(x)]]
The main point to be noted that f(x) and u (x) must be positive, otherwise their logarithms are not defined. This process of differentiation is known as logarithmic differentiation.

Derivative of a^x
Let y = a^x
Taking log of both sides,
log y = log (a^x )
log y = x log a
Differentiating both sides, w.r.t. x

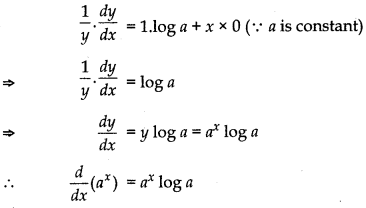
Derivative of log_a x
Let y = log_ax

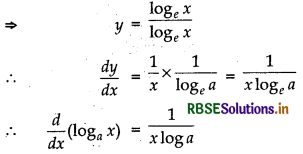
Derivatives Of Function In Parametric Form
Sometimes the relation between two variables is neither explicit nor implicit, but some link of a third variable with each of the two variables, separately, estabilishes a relation between the first two variables. In such a situation, we say that the relation between them is expressed via a third variable, which is called the parameter. More precisely, a relation expressed between two variables x and y in the form x -f(t), y = g(t) is said to be parametric form with t as a parameter.

In order to find derivative of function in such form, we have by chain rule.

Second Order Derivative
If y = f(x)
Then \(\frac{d y}{d x}=\frac{d}{d x}\)[f(x)] = f'(x) ........(1)
If f(x) is differentiable, we may differentiate (1) w.r.t. x
Then \(\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{d}{d x}\)[f'(x)]
Here \(\frac{d}{d x} \cdot\left(\frac{d y}{d x}\right)\) is called the second order derivative of y w.r.t. x and is denoted by \(\frac{d^{2} y}{d x^{2}}\). The second order derivative of f(x) is also denoted by f"(x). It is also denoted by D² or y"or y².

Mean Value Theorem:
In this section, we will state two fundamental result in calculus without proof. We shall also learn the geometric interpretation of these theorems.

Theorem:
(Rolle's Theorem) Let f: [a, b] → R be continuous on [a, b] and differentiable on (a, b), such that f(a) = f(b), where a and b are some real numbers Then there exists some c in (a, b) such that f' (c) = 0.

In the following figures graphs of a few typical dif-ferentiable functions satisfying the hypothesis of Rolle's

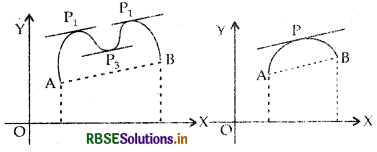
Observe what happens to the slope of the tangent to the curve at various point between r? and b. In each of the graphs, the slope becomes zero at least at one point. That is precisely the claim of the Rolle's theorrn as the slope of the tangent at any point on the graph of y = f(x) is nothing but the derivative of f(x) at that point.

Theorem :
(Mean Value Theorem) Let f: [a, b] → Rbeacontinuous function on [a, b] and differ¬entiable on (a, b). Then there exists some t in (a. b) such that
f'(c) = \(\frac{f(b)-f(a)}{b-a}\)

Observe that the Mean Value Theorem (MVT) is an extension of Rolle's theorem. Let us now understand a geo-metric interpretation of the MVT. The graph of a function y = f (x) is given in the following figure. We have already interpreted f '(c) as the slope of the tangent to the curve y = f(x) at (c, f(c)).

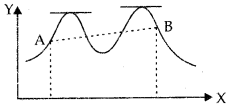
From the figure it is clear that \(\frac{f(b)-f(a)}{b-a}\) is the slope of the secant drawn between (a,f(a)) and (b,f(b)). The MVT states that there is a point c in (a, b) such that the slope of the tangent at (c, f(c)) is same as the slope of the secant between (a, f (a)) and (b, f(b)). in other words, there is a point c in (a, b) such that the tangent at (c, f(c)) is parallel to the secant between (a, f(a)) and (b,f(b)).

→ A real valued function is continuous at a point in its domain if the limit of the function at the point equals the value of the function at the point. A function is continuous if it is continuous on the whole of its domain.

→ Sum, difference, product and quotient of continuous functions are continuous, i.e., if f and g are continuous functions, then
f(±g)(x) = f(x) ± g(x) is continuous
(f-g)(x) = f(x)-g(x) is continuous.

→ \(\left(\frac{f}{g}\right)\)(x) = \(\frac{f(x)}{g(x)}\) (where g(x) ≠ 0) is continuous.

→ Every differentiable function is continuous, but the converse is not true.

→ Chain rule is rule to differentiate composite of functions.
If f = vou, t = u(x) and if both \(\frac{d t}{d x}\) and \(\frac{d v}{d t}\) exist then
\(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)

→ Following are some of the standard derivatives (in appropriate domains).
\(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)
\(\frac{d}{d x}\)(cos^-1x) = -\(\frac{1}{\sqrt{1-x^2}}\)
\(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)
\(\frac{d}{d x}\)(cot^-1x) = -\(\frac{1}{1+x^2}\)
\(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{x \sqrt{x^2-1}}\)
\(\frac{d}{d x}\)(cosec^-1x) = -\(\frac{1}{x \sqrt{x^2-1}}\)
\(\frac{d}{d x}\)(e^x) = e^x
\(\frac{d}{d x}\)(log x) = \(\frac{1}{x}\)

→ Logarithmic differentiation is a powerful technique to differentiate functions of the form f(x) = [u(x)]u(x). Here both f(x) and u(x) need to be positive for this technique to make sense.

→ Rolle's Theorem : If f: [a, b] → R is continuous on [a, b] and differentiable on (a, b) such that f(a) = f(b), then there exists some c in (a, b) such that f(c) = 0.

→ Mean Value Theorem: If f: [a, b] → R is continuous on [a, fr] and differentiable on (a, b). Then there exists some c in (a, b) such that
f(c) = \(\frac{f(b)-f(a)}{b-a}\)