RBSE Class 12 Maths Important Questions Chapter 4 सारणिक

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 4 सारणिक Important Questions and Answers.

RBSE Class 12 Maths Chapter 4 Important Questions सारणिक

अन्य महत्वपर्ण प्रश्न

प्रश्न 1.
सारणिक \(\left|\begin{array}{cc} \cos 50^{\circ} & \sin 10^{\circ} \\ \sin 50^{\circ} & \cos 10^{\circ} \end{array}\right|\) का मान है
(A) 0
(B) 1
(C) \(\frac{1}{2}\)
(D) - \(\frac{1}{2}\)
उत्तर:
(C) \(\frac{1}{2}\)

हल:
cos 50°cos 10° - sin 10° sin 50°
= cos(50° + 10°) = cos 60° = \(\frac{1}{2}\)
अतः सही विकल्प (C) है।

प्रश्न 2.
यदि w इकाई का एक घनमूल हो, तो सारणिक \(\left|\begin{array}{ccc} 1 & w^4 & w^8 \\ w^4 & w^8 & 1 \\ w^8 & 1 & w^4 \end{array}\right|\) का मान है
(A) w²
(B) w
(C) 1
(D) 0
उत्तर:
(D) 0

हल:
यदि w इकाई का एक घनमूल हो तब w³ = 1
1 + w + w² = 0 होता है

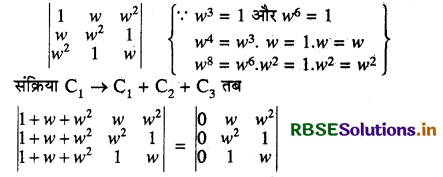
यहाँ पर C, के सभी अवयव शून्य हैं इसलिए सारणिक का मान शून्य होगा।
अतः सही विकल्प (D) है।

प्रश्न 3.
सारणिक \(\left|\begin{array}{cc} 1 & \log _b a \\ \log _a b & 1 \end{array}\right|\) =
(A) 1
(B) 0
(C) log_ab
(D) log_b a
उत्तर:
(B) 0

हल:
1 - log_ba × log_ab = 1 - log_aa = 1 - 1 = 0
∵ log_aa = 1
अतः सही विकल्प (B) है।

प्रश्न 4.
सारणिक, \(\left|\begin{array}{ccc} x+y & y+z & z+x \\ z & x & y \\ 2 & 2 & 2 \end{array}\right|\) का मान है
(A) x + y + z
(B) 2 (x + y + z)
(C) 1
(D) 0
उत्तर:
(D) 0

हल:
R₁ → R₁ + R₂ संक्रिया करने पर

R₃ के सभी अवयव शून्य हैं इसलिए सारणिक का मान शून्य होगा।
अतः सही विकल्प (D) है।

प्रश्न 5.
सारणिक \(\left|\begin{array}{lll} 6 & 6 & 6 \\ 6 & 6 & 6 \\ 6 & 6 & 6 \end{array}\right|\) का मान होगा
(A) 6
(B) 36
(C) 0
(D) 1
उत्तर
(C) 0

हल:
R₃ → R₃ - R₁ संक्रिया करने पर
\(\left|\begin{array}{lll} 6 & 6 & 6 \\ 6 & 6 & 6 \\ 0 & 0 & 0 \end{array}\right|\) = 0 चूँकि R₃ के सभी अवयव शून्य हैं।
अतः सही विकल्प (C) है।

प्रश्न 6.
\(\left|\begin{array}{lll} a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c \end{array}\right|\) बराबर होगा
(A) 4abc
(B) abc
(C) 0
(D) 2abc
उत्तर:
(C) 0

हल:
R₁ → R₁ + R₂ + R₃ संक्रिया करने पर
\(\left|\begin{array}{ccc} 0 & 0 & 0 \\ b-c & c-a & a-b \\ c-a & a-b & b-c \end{array}\right|\) = 0
चूँकि R₁ के सभी अवयव शून्य हैं।
अतः सही विकल्प (C) है।

प्रश्न 7.
यदि A = \(\left[\begin{array}{ll} 0 & 1 \\ 1 & 2 \end{array}\right]\) हो, तो adj A होगा-
(A) \(\left[\begin{array}{cc} 2 & -1 \\ -1 & 0 \end{array}\right]\)
(B) \(\left[\begin{array}{cc} 2 & -1 \\ -2 & 0 \end{array}\right]\)
(C) \(\left[\begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array}\right]\)
(D) \(\left[\begin{array}{cc} -2 & -1 \\ -1 & 0 \end{array}\right]\)
उत्तर:
(A) \(\left[\begin{array}{cc} 2 & -1 \\ -1 & 0 \end{array}\right]\)

हल:
A₁₁ = 2 A₁₂ = - 1 A₂₁ = - 1 A₂₂ = 0
adj A = \(\left[\begin{array}{ll} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right]^{\prime}=\left[\begin{array}{cc} 2 & -1 \\ -1 & 0 \end{array}\right]^{\prime}=\left[\begin{array}{cc} 2 & -1 \\ -1 & 0 \end{array}\right]\)
अतः सही विकल्प (A) है।

प्रश्न 8.
यदि A = \(\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]\) हो, तो A^-1 का मान होगा-
(A) \(\left[\begin{array}{ll} 4 & 2 \\ 3 & 1 \end{array}\right]\)
(B) \(\left[\begin{array}{cc} -2 & 1 \\ \frac{3}{2} & -1 / 2 \end{array}\right]\)
(C) \(\left[\begin{array}{cc} 4 & -3 \\ 2 & 1 \end{array}\right]\)
(D) \(\left[\begin{array}{ll} -4 & 3 \\ -2 & 1 \end{array}\right]\)
उत्तर:
(B) \(\left[\begin{array}{cc} -2 & 1 \\ \frac{3}{2} & -1 / 2 \end{array}\right]\)

हल:
A₁₁ = 4, A₁₂ = - 3, A₂₁ = - 2, A₂₂ = 1

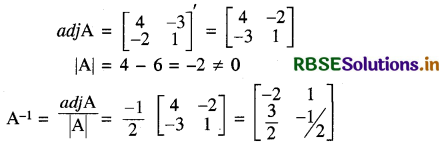
अतः सही विकल्प (B) है।

प्रश्न 9.
समान कोटि के वर्ग आव्यूह A, B, C के लिए AB = AC ⇒ B = C हो, तो A होगा-
(A) अव्युत्क्रमणीय आव्यूह
(B) अशून्य आव्यूह
(C) इकाई आव्यूह
(D) व्युत्क्रमणीय आव्यूह
उत्तर:
(D) व्युत्क्रमणीय आव्यूह
चूँकि व्युत्क्रमणीय आव्यूह में |A| ≠ 0

प्रश्न 10.
यदि A = \(\left[\begin{array}{cc} \cos x & \sin x \\ -\sin x & \cos x \end{array}\right]\) तथा A (adj A) = KI तो K का मान होगा-
(A) 3
(B) 2
(C) 1
(D) sin x . cos x
उत्तर:
(C) 1

हल:

प्रश्न 11.
यदि A = \(\left[\begin{array}{ccc} 3 & -1 & 2 \\ 2 & 1 & 3 \\ 1 & -3 & \mathrm{~K} \end{array}\right]\) एक अव्युत्क्रमणीय आव्यूह हो, तो। K का मान होगा-
(A) 2
(B) - 2
(C) 1
(D) - 1
उत्तर:
(B) - 2

हल:
एक अव्युत्क्रमणीय आव्यूह के लिए
|A| = 0 ∴ \(\left|\begin{array}{ccc} 3 & -1 & 2 \\ 2 & 1 & 3 \\ 1 & -3 & K \end{array}\right|\) = 0
3 (K + 9) + 1(2K - 3) + 2 (- 6 - 1) = 0
⇒ 3K + 27 + 2K - 3 - 14 = 0
⇒ 5K + 10 = 0 ⇒ K = - 2
अतः सही विकल्प (B) है।

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि \(\left|\begin{array}{ccc} \lambda+1 & 1 & 1 \\ 1 & 1 & -1 \\ -1 & 1 & 1 \end{array}\right|\) = 4 हो, तो λ का मान लिखिए।
हल:
(λ + 1) (1 + 1) - 1 (1 - 1) + 1 (1 + 1) = 4
⇒ 2λ + 2 - 0 + 2 = 4
⇒ λ = 0

प्रश्न 2.
यदि किसी सारणिक में कोई दो पंक्तियाँ या दो स्तम्भ सर्वसम हों, तो सारणिक का मान कितना होगा?
उत्तर:
सारणिक का मान शून्य होगा।

प्रश्न 3.
सारणिक \(\left|\begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+b \end{array}\right|\) का मान लिखिए।
हल:
= 1 {(1 + a) (1 + b) - 1} - 1 (1 + b - 1) + 1 (1 - 1 - a)
= 1 + a + b + ab - 1 - b - a
= ab

प्रश्न 4.
सिद्ध कीजिये कि \(\left|\begin{array}{cc} x^2+x+1 & x+1 \\ x & x-1 \end{array}\right|\) = x³ - x² - x - 1
हल:
माना कि ∆ = \(\left|\begin{array}{cc} x^2+x+1 & x+1 \\ x & x-1 \end{array}\right|\)
सारणिक का प्रसार करने पर
∆ = (x² + x + 1) (x - 1) - (x + 1)x
= x³ - 1 - x² - x = x³ - x² - x - 1

प्रश्न 5.
यदि A = \(\left[\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}\right]\) हो, तो A + A' का मान लिखिए।
हल:

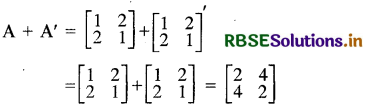
प्रश्न 6.
निम्न रैखिक समीकरण निकाय को मैट्रिक्स समीकरण के रूप में व्यक्त कीजिए
x + y + z = 6
x - y + z = 2
2x + y - z = 1
हल:
\(\left[\begin{array}{ccc} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} 6 \\ 2 \\ 1 \end{array}\right]\)

प्रश्न 7.
यदि A = \(\left[\begin{array}{ll} 3 & 2 \\ 1 & 4 \end{array}\right]\) हो, तो A . (adj A) का मान लिखिए।
हल:
A₁₁ = 4, A₁₂ = - 1, A₂₁ = - 2, A₂₂ = 3

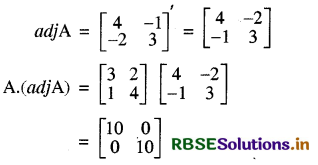
प्रश्न 8.
यदि A = \(\left[\begin{array}{cc} 3 & -3 \\ 3 & 3 \end{array}\right]\). B = \(\left[\begin{array}{ll} 6 & 3 \\ 4 & 2 \end{array}\right]\) तथा C = \(\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]\) हो, तो
व्युत्क्रमणीय मैट्रिक्स कौन-कौन से होंगे? लिखिए।
हल:
यहाँ पर |A| ≠ 0, |B| = 0, |C| ≠ 0
अतः व्युत्क्रमणीय मैट्रिक्स
A = \(\left[\begin{array}{cc} 3 & -3 \\ 3 & 3 \end{array}\right]\) तथा C = \(\left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]\) होंगे।

प्रश्न 9.
मैट्रिक्स रूप \(\left[\begin{array}{lll} 5 & 3 & 1 \\ 2 & 1 & 3 \\ 1 & 2 & 4 \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} 16 \\ 19 \\ 25 \end{array}\right]\) को रैखिक सरलीकरण निकाय के रूप में लिखिये।
हल:
5x + 3y + 2 = 16
2x + y + 37 = 19
x + 2y + 4z = 25

प्रश्न 10.
यदि A और B दो n क्रम के व्युत्क्रमणीय आव्यूह हों, तो (AB)^-1 का मान किसके बराबर होता है?
उत्तर:
(AB)^-1 = B^-1A^-1 के बराबर होता है।

प्रश्न 11.
यदि \(\left|\begin{array}{ll} 3 x & 7 \\ -2 & 4 \end{array}\right|=\left|\begin{array}{ll} 8 & 7 \\ 6 & 4 \end{array}\right|\) तब x का मान ज्ञात कीजिए।
हल:
\(\left|\begin{array}{ll} 3 x & 7 \\ -2 & 4 \end{array}\right|=\left|\begin{array}{ll} 8 & 7 \\ 6 & 4 \end{array}\right|\)
⇒ 12x + 14 = 32 - 42
⇒ 12x = - 24
⇒ x = - 2

लघूत्तरात्मक प्रश्न

प्रश्न 1.
दिखाइये कि
\(\left|\begin{array}{ccc} 1 & a & b \\ -a & 1 & c \\ -b & -c & 1 \end{array}\right|\) = 1 + a² + b² + c²
हल:
पंक्ति R₁ से प्रसार करने पर
= 1(1 + c²) - a (- a + bc) + b(ac + b)
= 1 + c² + a² - abc + abc + b²
= 1 + a² + b² + c²

प्रश्न 2.
सारणिक \(\left|\begin{array}{lll} 23 & 12 & 11 \\ 36 & 10 & 26 \\ 63 & 26 & 37 \end{array}\right|\) का मान प्रसार किये बिना ज्ञात कीजिये।
हल:
संक्रिया C₁ → C₁ - C₂ से करने पर
\(\left|\begin{array}{lll} 11 & 12 & 11 \\ 26 & 10 & 26 \\ 37 & 26 & 37 \end{array}\right|\) = 0
चूँकि C₁ तथा C₃ आपस में समान हैं।

प्रश्न 3.
निम्नलिखित सारणिक का प्रसार किये बिना, दर्शाइये कि \(\left|\begin{array}{rrr} 224 & 555 & 32 \\ 735 & 666 & 105 \\ 812 & 777 & 116 \end{array}\right|\) = 0
हल:

प्रश्न 4.
निम्नलिखित सारणिक का प्रसार किये बिना, दर्शाइये कि \(\left|\begin{array}{ccc} 0 & 51 & 65 \\ -51 & 0 & 79 \\ -65 & -79 & 0 \end{array}\right|\) = 0
हल:
माना कि ∆ = \(\left|\begin{array}{ccc} 0 & 51 & 65 \\ -51 & 0 & 79 \\ -65 & -79 & 0 \end{array}\right|\) ....... (1)
हम जानते हैं कि यदि किसी सारणिक की पंक्तियों और स्तम्भों को परस्पर बदल दिया जाये तो सारणिक का मान अपरिवर्तित रहता है। इसलिये
∆ = \(\left|\begin{array}{ccc} 0 & -51 & -65 \\ 51 & 0 & -79 \\ 65 & 79 & 0 \end{array}\right|\)
प्रत्येक स्तम्भ से (-1) उभयनिष्ठ लेने पर।
∆ = (- 1)³ \(\left|\begin{array}{ccc} 0 & 51 & 65 \\ -51 & 0 & 79 \\ -65 & -79 & 0 \end{array}\right|\)
∆ = (-1)³∆ = - ∆
∴ ∆ + A = 0
2∆ = 0
अतः ∆ = 0
या \(\left|\begin{array}{ccc} 0 & 51 & 65 \\ -51 & 0 & 79 \\ -65 & -79 & 0 \end{array}\right|\) = 0

प्रश्न 5.
यदि A, B, C किसी त्रिभुज के कोण हों, तो सिद्ध कीजिये कि
\(\left|\begin{array}{ccc} -1 & \cos C & \cos B \\ \cos C & -1 & \cos A \\ \cos B & \cos A & -1 \end{array}\right|\) = 0
हल:
स्तम्भ C₁ को a, C₂ को b तथा C₃ को c से गुणा करने तथा सारणिक को abc से भाग देने पर (जिससे कि मान अपरिवर्तित रहे)

प्रश्न 6.
यदि A तथा B एक ही क्रम के व्युत्क्रमणीय वर्ग मैट्रिक्स हैं तो सिद्ध कीजिए कि
(AB)^-1 = B^-1. A^-1
हल:
यदि A व्युत्क्रमणीय है तो परिभाषा के अनुसार यह वर्ग मैट्रिक्स होगा। अत: A एवं B एक ही क्रम का वर्ग मैट्रिक्स है तथा इसे गुणन AB भी सम्भव होगा।
क्योंकि
|A| ≠ 0, |B| ≠ 0
∴ AB = |A| B ≠ 0
अतः मैट्रिक्स AB भी व्युत्क्रमणीय है।
अब एक मैट्रिक्स C इस प्रकार लें कि
C = B^-1 A^-1
∴ (AB)C = (AB) (B^-1 A^-1)
= A . (BB^-1)A^-1 (साहचर्यता)
= A . IA^-1 [∵ BB-1 = I]
= AA^-1 = I
इसी प्रकार C(AB) = (B^-1 A^-1) AB
= B^-1 (A^-1A)B
= B^-1(I)B [∵ A^-1A = I]
= B^-1B
= I
∴ (AB)C = I = C(AB)
अतः मैट्रिक्स AB का एकमात्र व्युत्क्रम मैट्रिक्स C है।
∴ (AB)^-1 = C = B^-1 A^-1

प्रश्न 7.
सारणिक के गुणधर्मों का प्रयोग करके सिद्ध कीजिए
\(\left|\begin{array}{ccc} 2 y & y-z-x & 2 y \\ 2 z & 2 z & z-x-y \\ x-y-z & 2 x & 2 x \end{array}\right|\) = (x + y + z)³
हल:

C₂ → C₂ - C₁ तथा C₃ → C₃ - C₁ द्वारा
L.H.S. = (x + y + z)

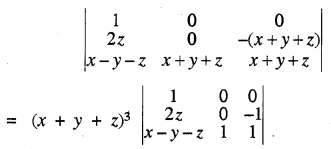
= (x + y + z)³ [1 (0 + 1)]
= (x + y + z)³ = R.H.S.

निबन्धात्मक प्रश्न

प्रश्न 1.
सारणिकों को बिना विस्तार किये हुए, सिद्ध कीजिए कि

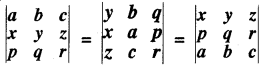
हल:

प्रश्न 2.
मैट्रिक्स \(\left[\begin{array}{ccc} 3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2 \end{array}\right]\) की व्युत्क्रम मैट्रिक्स ज्ञात कीजिये तथा इसके पश्चात् इसकी सहायता से निम्नलिखित समीकरण निकाय को हल कीजिये-

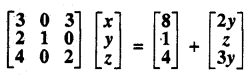
हल:
माना A = \(\left[\begin{array}{ccc} 3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2 \end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ccc} 3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2 \end{array}\right|\)
= 3(2 - 3) + 2(4 + 4) + 3(- 6 - 4)
∴ A = -3 + 16 - 30 = -17 .......(1)
∵ |A| ≠ 0 ∴ A^-1 का अस्तित्व है।
सारणिक |A| के अवयवों के संगत सहखण्डों से निर्मित मैट्रिक्स होगी

प्रश्न 3.
सिद्ध कीजिये कि
\(\left|\begin{array}{ccc} a+b+2 c & c & c \\ a & b+c+2 a & a \\ b & b & c+a+2 b \end{array}\right|\) = 2(a + b + c)³.
हल:

∆ = 2(a + b + c) ((a + b + c)² - 0)
= 2(a + b + c)³

प्रश्न 4.
सारणिकों के गुणधर्मों का प्रयोग कर सिद्ध कीजिए कि
\(\left[\begin{array}{lll} a^3 & 2 & a \\ b^3 & 2 & b \\ c^3 & 2 & c \end{array}\right]\) = 2 (a - b) (b-c) (c - a) (a + b + c)
हल:

∆ = - 2 (a - b) (b - c) (a² + ab + b² - b² - bc - c²)
= - 2a - b) (b - c) (a² - c² + ab - bc)
= - 2(a - b) (b - c) ((a + c) (a - c) + b (a - c))
= - 2(a - b) (b - c) (a - c) (a + b + c)
∴ ∆ = 2(a - b) (b - c) (c - a) (a + b + c)