RBSE Class 12 Chemistry Notes Chapter 4 रासायनिक बलगतिकी

These comprehensive RBSE Class 12 Chemistry Notes Chapter 4 रासायनिक बलगतिकी will give a brief overview of all the concepts.

RBSE Class 12 Chemistry Chapter 4 Notes रासायनिक बलगतिकी 

→ आयनिक या तात्कालिक अभिक्रियाएं (Ionic or Instantaneous Reactions):
वे अभिक्रियाएँ जो आयनों के मध्य होती हैं एवं अत्यधिक तीव्र वेग के साथ सम्पन्न होती हैं आयनिक अभिक्रियाएँ कहलाती हैं। उदाहरणार्थ
NaCl_(aq) + AgNO_3(aq) → AgCl_(s) +NaNO_3(aq)
या Cl^- + Ag⁺ → AgCl↓

→ अति मन्द अभिक्रियाएँ (Very Slow Reactions):
ये अभिक्रियाएँ अणुओं के मध्य होती है। इनकी गति अत्यधिक मन्द होती है अतः इनमें कोई दर्शनीय या मापनीय परिवर्तन नहीं होता है। उदाहरणार्थ-उत्प्रेरक की अनुपस्थिति में हाइड्रोजन व ऑक्सीजन के संयोग से जल बनने की क्रिया।।

→ आण्विक या मन्द अभिक्रियाएँ (Molecular or Slow Reactions):
वे अभिक्रियाएँ जो अणुओं के मध्य होती हैं, आण्विक अभिक्रियाएँ कहलाती हैं। इनके वेग ज्ञात किये जा सकते हैं।

उदाहरणार्थ
(i) अम्ल और ऐल्कोहॉल की क्रिया द्वारा ऐस्टर का निर्माण।
CH₃COOH_(aq) + C₂H_5(aq)OH ⇌ CH₃COOC₂H_5(aq) +H₂O_(l)

(ii) क्लोरोफॉर्म का प्रकाश द्वारा ऑक्सीकरण

→ अभिक्रिया वेग (Rate of Reaction):
एकांक समय में किसी अभिकारक अथवा उत्पाद की सान्द्रता में हुए परिवर्तन को अभिक्रिया का वेग कहते हैं। इसका मात्रक mol L^-1s^-1 (मोल प्रति लीटर प्रति सेकण्ड) होता है।

→ औसत वेग (Average Rate):
किसी रासायनिक अभिक्रिया में उपस्थित अभिकारक या उत्पाद की सान्द्रता में एकांक समय में होने वाले परिवर्तन को उस अभिक्रिया का औसत वेग (Average rate) कहते हैं।

→ तात्कालिक वेग (Instantaneous Rate):
किसी निश्चित क्षण पर अभिक्रिया का वास्तविक वेग तात्क्षणिक वेग या तात्कालिक वेग कहलाता है।

→ ताप गुणांक (Temperature Coefficient):
25°C तथा 35°C ताप पर या 10°C ताप के अन्तर पर अभिक्रिया के वेग नियतांकों का अनुपात ताप गुणांक कहलाता है। इसका मान लगभग 2 से 3 होता है।

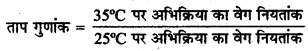
→ वेग नियम अथवा वेग व्यंजक (Rate law or Rate Expression):
वह समीकरण जो अभिक्रिया वेग एवं अभिकारकों की सान्द्रता में सम्बन्ध स्थापित करता है, वेग नियम कहलाता है।
उदाहरणार्थ- aA+bB → cC+ dD अभिक्रिया के लिये वेग नियम के अनुसार
अभिक्रिया का वेग (r) = k[A]^a [B]^b

→ अभिक्रिया की आण्विकता या अणुसंख्यता (Molecularity of Reaction):
अभिक्रिया के किसी पद में भाग लेने वाले अभिकारकों के अणुओं की कुल संख्या अभिक्रिया की आण्विकता या अभिक्रिया की अणुसंख्यता कहलाती है।

→ सरल अभिक्रियाएँ (Simple Reactions):
ऐसी अभिक्रियाएँ जिनकी आण्विकता उनके अभिकारकों की संख्या के बराबर होती है सरल अभिक्रियाएँ कहलाती हैं।
उदाहरण-O₂F₂ → O₂ + F₂ (आण्विकता = 1)

→ जटिल अभिक्रियाएँ (Complex Reactions):
ऐसी अभिक्रियाएं जिनमें अभिकारकों की संख्या तीन से ज्यादा होती है। ये अभिक्रियाएँ साधारणतः दो या अधिक पदों में सम्पन्न होती हैं इन अभिक्रियाओं में मन्द गति का पद वेग निर्धारक पद (Rate determining step) कहलाता है। ये अभिक्रियाएँ जटिल अभिक्रियाएँ कहलाती है। उदाहरणार्थ
Br + O₂ → 2H₂O + 2Br₂
वेग =k [HBr] [O₂]

→ अभिक्रिया की कोटि (Order of Reaction):
किसी अभिक्रिया में भाग लेने वाले अभिकारक अणुओं की वह संख्या जिसकी सान्द्रता परिवर्तन से अभिक्रिया के वेग का निर्धारण किया जाता है, अभिक्रिया की कोटि कहलाती है।

→ अर्द्ध-आयुकाल (Half Life Period):
अभिक्रिया में अभिकारक के आधे भाग को उत्पाद में परिवर्तित करने में जितना समय लगता है उसे उस अभिक्रिया का अर्द्ध आयुकाल (t½) कहते हैं।

→ छद्म एकाणुक अभिक्रियाएँ (Pseudo Unimolecular Reactions):
ऐसी अभिक्रियाएँ जिनकी अणुसंख्यता दो या अधिक हो परन्तु कोटि एक हो, छद्म एकाणुक अभिक्रियाएँ (Pseudo unimolecular reactions) कहलाती हैं।
उदाहरणार्थ

→ सक्रियण ऊर्जा (Activation Energy):
अभिकारक अणुओं की औसत ऊर्जा (Average energy) से अधिक वह निश्चित न्यूनतम ऊर्जा जो अणुओं के टकराने पर प्रभावी टक्कर होने के लिये अणुओं में उपस्थित होना अनिवार्य है, सक्रियण ऊर्जा कहलाती है।
E = E_r - E_R
E_a = सक्रियण ऊर्जा, E_T = देहली ऊर्जा, E_R = अभिकारकों की औसत ऊर्जा

→ संघट्ट आवृत्ति (Collision Frequency):
किसी अभिक्रिया मिश्रण के प्रति इकाई आयतन में प्रति सेकण्ड होने वाली टक्करों को संघट्ट आवृत्ति कहा जाता है।

→ आंशिक दाब तथा मोल की संख्या में सम्बन्ध गैस A का आंशिक दाब

→ शून्य कोटि की अभिक्रिया के लिये दर नियम
A + B → C + D
\(\frac{dx}{dt}\) = k[A]°[B]
वेग स्थिरांक (K) की विमा = mol L^-1 s^-1
t_½ ∝ P
यहाँ 'P' प्रारम्भिक सान्द्रता है ।
t_½ = अर्द्ध-आयु

→ शून्य कोटि की अभिक्रिया के लिये समाकलित वेग समीकरण
k = \(\frac{[\mathrm{A}]_0-[\mathrm{A}]}{t}\)
(अर्द्ध-आयु) t_½ = \(\frac{[\mathrm{A}]_0}{2 k}=\frac{a}{2 k}\)

→ प्रथम कोटि की अभिक्रिया के लिये समाकलित वेग समीकरण
k = \(\frac{2 \cdot 303}{t}\) log \(\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
अर्द्ध-आयु (t_½) = \(\frac{0 \cdot 693}{k}\)

→ आर्हेनियस समीकरण
(a) k = Ae-^E_a/RT
(b) In k = In A - \(\frac{\mathrm{E}_a}{\mathrm{RT}}\)
(c) log k = logA - \(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)
(d) log\(\frac{k_2}{k_1}=\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\left(\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right)\)
यहाँ k₁ तथा k₂, ताप T₁ तथा T₂ पर वेग स्थिरांक हैं।

→ गैसीय अभिक्रिया के लिए
k = \(\frac{2 \cdot 303}{t} \)log \(\frac{\mathrm{P}_i}{2 \mathrm{P}_i-\mathrm{P}_t}\)

→ nवें अंश (fraction) के भाग पूर्ण होने में लगा समय-:
(t_1/n) = \(\frac{2 \cdot 303}{k}\) log \(\frac{1}{\left(1-\frac{1}{n}\right)}\)

→ अभिक्रिया aA + bB → cC + dD के लिये,
तात्क्षणिक वेग = -\(\frac{1}{a} \frac{d[\mathrm{~A}]}{d t}=-\frac{1}{b} \frac{d[\mathrm{~B}]}{d t}\)
= \(\frac{1}{c} \frac{d[\mathrm{C}]}{d t}=\frac{1}{d} \frac{d[\mathrm{D}]}{d t}\)

→ वेग स्थिरांक की इकाई (k) = (mol/L)^1-xs^-1

→ वेग स्थिरांक की इकाई (k) = (atm)^1-xs^-1
(यदि अभिकारक एवं उत्पाद दोनों ही गैस हैं।)