RBSE Class 11 Maths Notes Chapter 8 Binomial Theorem

These comprehensive RBSE Class 11 Maths Notes Chapter 8 Binomial Theorem will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 8 Notes Binomial Theorem

Introduction:
We have already read square and cube of expansions of Binomials as :

• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²
• (a + b)³ = a³ + 3 a²b + 3ab² + b³
• (a - b)³ = a³ - 3a²b + 3ab² - b³

The ancient Indian mathematicians knew about the coefficients in the expansion of (a + b)n in third century. The arrangement of this coefficients was in the form of a diagram called meru-prastara provided by Pingla. In sixteenth century, Bombelli also gave the coefficients in the expansion of (a + b)ⁿ, n < 7 and Oughtred gave them for n = 1, 2, ............... 10 in the starting of seventeenth century.

After this the triangle, popularly known as ‘Pascal’s triangle was constructed by the French Mathematician Blaise Pascal, which is of the following type :

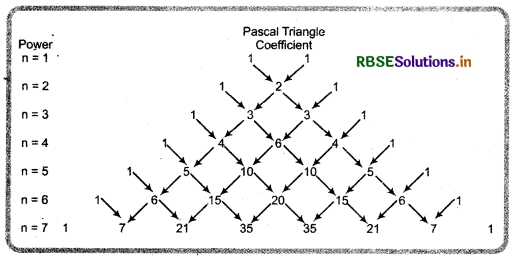
In Pascal triangle each row start and end with in the beginning and the end numbers lie on same distances are equal. Any number of any line is obtained by adding those two numbers of previous line which lie on left and right side of number. Each row bounded by 1 on both side.

Binomial Expansion:
Any algebraic expression with two terms is called binomial expansion or only Binomial. Two terms are joined by positive or negative sign.
For Example :
(i) x + a, here x is first term and a is second term.
(ii) x² - 9 etc.
Binomial Theorem: The formula by which any power of Binomial expression is expanded in the form of a series is called Binomial Theorem. Binomial Theorem is used to expand binomial expansion.
Binomial Coefficient: In the expansion of Binomial expansion (x + a)ⁿ, coefficients of different powers of x are called Binomial coefficients.
Similarly, It can be extended for more powers.

Coefficients of Terms of Binomial Expansion
In the expansion of Binomial exponents, to write coefficient of terms, symbol of combination ⁿC_r is used, as given in above table. If we expand (a + b) for power 8 then in (a + b)⁸ coefficient of 4th term according to table = ⁸C₃ = 56.
Thus, in (a + b)ⁿ coefficient of (r + 1)th term = ⁿC_r Term of its expansion can be seen from above table.
In more generalised form, Binomial expansion of (x + y)ⁿ can be written in following theorem form, where n is a positive integer.

Binomial Theorem for Positive Integer n
(x + a)ⁿ = ⁿC₀ xⁿ + ⁿC₁ x^n-1a + ⁿC₂ x^n-ra² + .... + ⁿC_r x^n-r a^r + .... + ⁿC_n aⁿ

Mathematical Analysis
Proof : We will prove this theorem by mathematical induction
(x + a)¹ = x + a = ¹C₀x¹ + ¹C₁ x^1-1a .............(1)
(x + a)² = x² + 2ax + a² = ²C₀x² + 2C₁ x^2-1a + ²C₂x^2-2a² ..........(2)
From (1) and (2), it is clear that theorem is true for n = 1 and 2. Let theorem is true for +ve Integer m.
Then,
(x + a)^m = ^mC₀x^m + ^mC₁ x^m-1a + ^mC₂ x^m-2a² + ... + ^mC_r x^m-r ar + ...+ ^mCm a^m
Multiplying both sides by (x + a)
(x + a)(x + a)^m = (x + a) [^mC₀x^m + ^mC₁ x^m-1a + ^mC₂ x^m-2a² + ...+ ^mC_rx^m-r a^r + ... + ^mC_m a^m]
(x + a)^m+1 = x[^mC₀ x^m + ^mC₁ x^m-1a + ^mC₂x^m-2 a² + ... + ^mC_r x^m-r a^r + ... + ^mC_m a^m] + a[mC₀x^m + ^mC₁ x^m-1a + ^mC₂x^m-2 a² + ... + ^mC_r x^m-r a^r + ... + ^mC_m a^m]
= ^mC₀ x^m+1 + (^mC₁ + ^mC₀)x^ma + (^mC₂ + ^mC₁)x^m-1 a² + (^mC₃ + ^mC₂)x^m-2a³ +... + (^mC_r + ^mC_r-1)x^m-r+1 a^r + ... + ^mC_ma^m+1
mC₁ + ^mC₀ = ^m+1C₁,
^mC₂ + ^mC₁ = ^m+1C₂,
.... .............. .............
.... .............. .............
^mC_r + ^mC_r-1 = ^m+1C_r
and ^mC_m = ^m+1C_m+1 = ^mC₀ = ^m+1C₀ = 1
Thus, (x + a)^m+1 = ^m+1C₀ x^m+1+ ^m+1C₁x^ma + ^m+1C₂x^m-1a² + ... + + 1C_rx^m-r+1a^r + ... + ^m+1C_m+1a^m+1 ............(4)
It is clear from (4) that theorem is true for n = m + 1.
Hence, by mathematical induction, this theorem is true for each positive integer i.e., if n is any positive integer, then
(x + a)ⁿ = ⁿC₀xⁿ + ⁿC₁ x^n-1 a + ⁿC₂x^n-2a² + ...+ ⁿC_rx^n-ra^r + ... + ⁿC_naⁿ
Note: Here ⁿC₀, ⁿC₁, ⁿC₂, ⁿC₃, ⁿC₄ ........... ⁿC_n are called binomial coefficients.

Various Important Forms of Binomial Theorem
(x + a)ⁿ = xⁿ + ⁿC₁ x^n-1a + ⁿC₂ x^n-2 a²+ ........ + ⁿC_rx^n-ra^r + ....+ aⁿ ...(1)
Replacing a by - a in (1)
(x - a)ⁿ = xⁿ - ⁿC₁ x^n-1 a + ⁿC₂ x^n-2a² -.... + (- 1)^{r n}C_r x^n-r a^r + .... + (- 1)ⁿ aⁿ ...(2)
Changing a and x to each other in (1)
(a + x)ⁿ = aⁿ + ⁿC₁ a^n-1x + ⁿC₂ a^n-2 + ......+ ⁿC_ra^n-rx^r +... + xⁿ ...(3)
In (3) putting -x in place of x
(a -x)ⁿ = aⁿ - ⁿC₁ a^n-1 x + ⁿC₂ a^n-2 x² + ........ (- 1)^r (a)^n-r x^r +....+ (-1)ⁿ xⁿ ...(4)
In (1) putting x = 1 and a = x
(1 + x)ⁿ = 1 + ⁿC₁x + ⁿC₂x² + ........+ ⁿC_rx^r + ...+ xⁿ ...(5)
In (1) putting x = 1 and a = - x
(1 - x)ⁿ = 1 - ⁿC₁x + ⁿC₂ x² - ....... + (- 1)^rnC_rx^r + ...+ (- 1)ⁿxⁿ ...(6)

General Term in Binomial Expansion
In the expansion (r + 1 )th term is called general term and denoted by T_r+1.
i.e., T_r+1 = ⁿC_ra^n-rb^r
Putting r = 1, 2, 3, ........ we can find first, second, ........term of the expansion which are denoted by T₁, T₂, T₃, T₄...........
Similarly,. T₁ = ⁿC₀ aⁿ
T₂ = ⁿC₁a^n-1b
T₃ = ⁿC₂ a^n-2b²
T₄ = ⁿC₃ a^n-3b³

Important Informations related to Binomial Expansion for Positive Integer Power

• In the expansion of (x + a)ⁿ, number of terms is 1 more than power i.e., (n + 1)
• In the expansion, power of x decreases and power of a increases in each term, sum of power of x and a is equal to power of binomial (n)
• Coefficients of the terms equally distant from the beginning and end of expansion, are equal i.e., ⁿC₀ = ⁿC_n = 1, ⁿC₁ = ⁿC_n-1, ⁿC₂ = ⁿC_n-2, ..............
  ⁿC_r = ⁿC_n-r (1 ≤ r ≤ n)

Example : Find general term or (r + 1)th term in expansion of (x² + \(\frac{1}{x}\))ⁿ where n is a natural number.
Verify your answer for first term of expansion.
Solution:
General term of expansion is obtained as follows:
Tr + l = ⁿC_r(x²)^n-r = ⁿC_rx^2n-2r
= ⁿC_rx^2n-3r ...(i)
Thus, in expansion (r+ l)th term is ⁿC_rx^2n-3r.
Expanding (x² + \(\frac{1}{x}\))ⁿ we see that 1st term is (x²)ⁿ or x²ⁿ.
Using (i) putting, r = 0 we get 1st term.
Since, T₁ = T₀₊₁
T₁ = ⁿc0x^2n-0 = x²ⁿ
It proves that for T_r+1 given expression is true for r +1 = 1.

Middle Term in Binomial Expansion of (x + a)ⁿ
1. If power n is even, then the number of terms in the expansion will be odd. Therefore, there will be one middle term.
Middle term = \(\left(\frac{n}{2}+1\right)=\left(\frac{n+2}{2}\right)=\left[\frac{(n+1)+1}{2}\right]\)
= \(\left(\frac{\text { No. of terms in expansion }+1}{2}\right)^{\text {th }}\) term

2. If power n is odd then the number of terms in the expansion will be even. Therefore, there will be two middle terms.
Middle term = \(\left(\frac{n+1}{2}\right)^{\text {th }} \)term and \(\left(\frac{n+1}{2}+1\right)^{\text {th }}\) term
= \(\left(\frac{n+3}{2}\right)^{\text {th }}\) term

Coefficient of Special Power x^m in Binomial Expansion
If n is a positive integer, then
(x - y)ⁿ = ⁿC₀ xⁿ - ⁿC₁ x^n-1y + ⁿC₂ x^n-2y² - ⁿC₃ x^n-3 y³ + ................ (-1)^{n-1 n}C_n-1 xy^n-1 + (-1)^{n n}C_nyⁿ
In this expansion, coefficient of specific power xm is find such that :
Step-1, Find (r + 1)th term i. e., T_r+1 or general term of given binomial expansion.
Step-2. After finding T_r+1 all variables and constants are solved in exponential form.
Step-3. The specific power whose coefficient has to find that exponential is equality to power of x and then find value of r.
Step-4. All possible values of r put in equation of T_r+1 and then solve and get coefficient of specific power.
Let in expansion of (ax^p ± \(\frac{b}{x^q}\))ⁿ if x^m comes is term T_(r+1)th then
T_r+1 = ⁿC_r(ax^p)^n-r\(\left(\pm \frac{b}{x^q}\right)^r\)
= ⁿC_ra^n-r(± b)^r x^np-r(p+q)
∴ Finding the value of r from np - r(p + q) = m then find special term, r is always positive integer.

Thus, coefficient of xm will be nCr an r (± b)^r
If we have to find term independent x in expansion,
np - r(p + q) = 0
r = \(\frac{n p}{p+q}\)

Example : In (x + 3)⁸ find coefficient of x⁵.
Solution:
Let in expansion of (x + 3)⁸ coefficient of x⁵ in (r + 1)th term will be x⁵.
Then, in expansion of (x + 3)⁸
(r + 1)th term = ⁸C_r x^8-r(3)^r
T_r+1 = ⁸C_r x^8-r3^r

Here power of x is 5, so x^8-r = x⁵
Comparing powers,
8 - r =5
∴ r = 8 - 5 = 3
then (r + 1)th term, T_r+1 = ⁸C₃ x⁵3³
Thus, coefficient of x⁵ = ⁸C₃ 3³

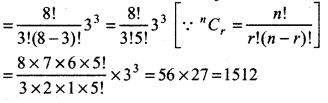
Thus, in expansion of (x + 3)⁸ coefficient of x⁵ = 1512.

Number of Terms in the Expansion of (a + b + c)ⁿ
v (a + b + c)ⁿ = [(a + b) + c]ⁿ
= (a + b)ⁿ + ⁿC₁ (a + b)^n-1 c + ⁿC₂ (a + b)^n-2 c² + .... + cⁿ
Number of terms in expansion of (a + b + c)ⁿ
= (n + 1) + n + (n - 1) term + .... + 1 term
= \(\frac{(n+1)(n+2)}{2}\) term

→ If n is positive integer power then number of terms in the expression of (x + a)ⁿ is (n + 1) and (x + a)ⁿ = ⁿC₀xⁿ + ⁿC₁ x^n-1a + ⁿC₂ x^n-2a² + ... + ⁿC_r x^n-ra^r + ... + ⁿC_naⁿ.

→ General term T_r+1 = ⁿC_rx^n-ra^r in the expansion of (x + a)ⁿ.

• If n is even then middle term\(\left(\frac{n}{2}+1\right)=\left(\frac{n+2}{2}\right)\)term,
• If n is odd, then middle term = \(\left(\frac{n+1}{2}\right)^{\text {th }}\) and \(\left(\frac{n+3}{2}\right)^{\text {th }}\) term.

→ The Binomial theorem for any power : (1 +x)ⁿ = 1 + nx + \(\frac{n(n-1)}{2 !}\) x² + \(\frac{n(n-1)(n-2)}{3 !}\) x³ + ..........
Here number of terms are infinite.

→ General term of series (1 + x)ⁿ = T_r+1 = \(\frac{n(n-1)(n-2) \ldots(n-r+1)}{r !}\) × x^r

→ There are (n +1) terms in the expansion of (a + b)ⁿ, more than one term of index.

→ Number of terms in

→ (1 + x)ⁿ = ⁿC_r x^r

→ ⁿC₀ + ⁿC₁ + ⁿC₂ + ............ + ⁿC_n = 2ⁿ

→ (1 + x)ⁿ = 1 + ⁿC₁ x + ⁿC₂ x² + ⁿC₃ x³ + ............ + ⁿC_n xⁿ

→ (1 - x)ⁿ = 1 - ⁿC₁ x + ⁿC₂ x² - ⁿC₃ x³ + .......... + (-1)ⁿC_n xⁿ