RBSE Class 11 Maths Notes Chapter 15 सांख्यिकी

These comprehensive RBSE Class 11 Maths Notes Chapter 15 सांख्यिकी will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 15 Notes सांख्यिकी

भूमिका (Introduction):
पिछली कक्षा में हमने केन्द्रीय प्रवृत्ति के मापों (माध्य, माध्यिका, बहुलक) का अध्ययन किया था। लेकिन सांख्यिकीय तथ्यों का विश्लेषण करके निष्कर्ष निकालने की प्रक्रिया में केन्द्रीय प्रवृत्ति के माप परिपूर्ण नहीं हैं। केवल इन्हीं मापों के प्रयोग के आधार पर निष्कर्ष निकालने पर बहुधा त्रुटि रह जाती है तथा भ्रामक परिणाम प्राप्त होते हैं । केन्द्रीय प्रवृत्तियों से हमें श्रेणी के केन्द्रीय मान का पता चलता है, जो श्रेणी का प्रतिनिधित्व करता है, लेकिन हमको इस बात की जानकारी प्राप्त नहीं होती है कि श्रेणी के विभिन्न मान केन्द्रीय मान के कितने पास हैं या कितने दूर फैले हुए हैं। उदाहरण के लिए निम्न सारणी में दिये गये विद्यार्थियों के तीन समूह के गणित विषय में प्राप्तांक इस प्रकार हैं-

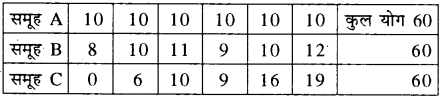
उपर्युक्त प्रत्येक समूह का माध्य 10 है परन्तु प्राप्तांकों के इन समूहों के आकार में बहुत अन्तर है । प्रथम समूह A के सभी प्राप्तांक समान हैं और उनका माध्य से कोई बिखराव नहीं है । अतः माध्य पूर्ण रूप से समूह का प्रतिनिधित्व कर रहा है। द्वितीय समूह B में प्राप्तांकों में भिन्नता है और माध्य से उनका विचलन 2 से अतः माध्य सभी पदों का यथोचित प्रतिनिधित्व नहीं कर रहा है । समूह C के प्राप्तांकों के माध्य से विचलन - 10 से + 9 के मध्य है जो बहुत अधिक है। अतः माध्य समूह C के प्राप्तांकों का उचित प्रतिनिधित्व नहीं कर रहा है । अत: श्रेणी के बारे में पूर्ण ज्ञान प्राप्त करने के लिए केन्द्रीय मान ही पर्याप्त नहीं है बल्कि विभिन्न चर के मानों का केन्द्रीय मान (Central Value) से औसत अन्तर श्रेणी की रचना तथा स्वरूप आदि की जानकारी भी आवश्यक है। इसके लिए इस अध्याय में हम श्रेणी के विभिन्न मानों के बिखराव के माप का अध्ययन करेंगे ।
किसी श्रेणी के पदों का माध्य से बिखराव को विक्षेपण (dispersion) कहते हैं । इस प्रकार हम कह सकते हैं कि विक्षेपण आँकड़ों के फैलाव को बताता है। विक्षेपण की मात्रा कम होने से तात्पर्य यह है कि उस श्रेणी के पदों का उनके माध्य से विचलन कम है । विक्षेपण की मात्रा अधिक होने से तात्पर्य यह है कि उस श्रेणी के पदों का उनके माध्य से विचलन अधिक है। अतः केवल माध्य की जानकारी होने से किसी श्रेणी के विषय में पूरी जानकारी नहीं हो सकती है । माध्य के साथ-साथ श्रेणी के विक्षेपण का ज्ञान होना भी आवश्यक है ।

प्रकीर्णन की माप (Measures of Dispersion):
केन्द्रीय प्रवृत्ति के किसी माप (माध्य, माध्यिका, बहुलक ) से बंटन के पदों के विचलनों के माप को विक्षेपण की माप (Measures of dispersion) कहते हैं ।
विक्षेपण के निम्नलिखित प्रमुख माप हैं-
(i) परिसर (Range)
(ii) चतुर्थ विचलन (Quartile Deviation)
(iii) माध्य विचलन (Mean deviation)
(iv) मानक विचलन एवं प्रसरण (Standard deviation and variance)
इस अध्याय में हम चतुर्थक विचलन के अतिरिक्त अन्य सभी मापों का अध्ययन करेंगे ।

परिसर (Range):
किसी श्रेणी में चर के उच्चतम मान (H) और निम्नतम मान (L) के अन्तर को परास (R) या परिसर या विस्तार कहते हैं ।
उदाहरणार्थ- यदि एक कक्षा के विद्यार्थियों में सबसे लम्बे विद्यार्थी की लम्बाई 70 इंच तथा सबसे छोटे विद्यार्थी की लम्बाई 56 इंच है तो कक्षा में विद्यार्थियों की लम्बाई का परास 70 - 56 = 14 इंच होगा।
यदि चर सतत श्रेणी के रूप में दिये गये हों तो सबसे बड़े वर्ग की उच्च सीमा तथा सबसे छोटे वर्ग की निम्न सीमा का अन्तर ही परास या परिसर या विस्तार कहलाता है ।
उदाहरणार्थ - यदि कोई श्रेणी 5-10, 10-15, 15-20, 20-25, 25-30, 30-35, 35-40 के वर्गों में विभाजित है तो श्रेणी का परास 40 - 5 = 35 होगा।
परास वास्तव में विक्षेपण का एक निरपेक्ष (Absolute) मान है, जो चर मूल्यों के केवल चरम मानों पर ही निर्भर करता है । अतः दो श्रेणियों के विक्षेपण की तुलना करने के लिए यह विधि विशेष उपयोगी नहीं है । जैसे एक श्रेणी बहुत बड़ी हो, दूसरी श्रेणी बहुत छोटी हो तो एक का परास अधिक होगा व दूसरे का कम । परन्तु यह भी हो सकता है कि जिसका परास कम है उसके चर मूल्यों में बिखराव असमान हो और जिसका परास अधिक है उसके चर मूल्यों में बिखराव में समानता हो ।

माध्य विचलन (Mean Deviation):
किसी भी श्रेणी में चर के विभिन्न मानों का, उसके सांख्यिकीय माध्य (समान्तर माध्य, माध्यिका एवं बहुलक) से लिए गए विचलनों के निरपेक्ष मानों का समान्तर माध्य उसका माध्य विचलन कहलाता है । अतः केन्द्रीय प्रवृत्ति 'a' के सापेक्ष माध्य विचलन प्रेक्षणों का 'a' से विचलनों के निरपेक्ष मानों का माध्य होता है । 'a' के सापेक्ष माध्य विचलन M.D. (a) द्वारा प्रकट किया जाता है।

टिप्पणी- माध्य विचलन केन्द्रीय प्रवृत्ति की किसी भी माप से ज्ञात किया जा सकता है । किन्तु सांख्यिकी अध्ययन में सामान्यतः माध्य और माध्यिका के सापेक्ष माध्य विचलन का उपयोग किया जाता है ।

अवर्गीकृत आँकड़ों के लिए माध्य विचलन (Mean deviation for ungrouped datas):
माना कि n प्रेक्षणों के आँकड़े x₁, x₂, x₃ .......... x_n दिये गये हैं। माध्य या माध्यिका के सापेक्ष माध्य विचलन के मान की गणना करते समय निम्नलिखित चरण प्रयुक्त होते हैं-
चरण 1. उस केन्द्रीय प्रवृत्ति की माप को ज्ञात कीजिए जिसकी सहायता से हमें माध्य विचलन ज्ञात करना है। माना कि वह माप 'a' है ।
चरण 2. प्रत्येक प्रेक्षण x का a से विचलन अर्थात् x₁ - a, x₂ - a, x₃ - a, .............. x_n - a ज्ञात करते हैं।
चरण 3. अब विचलनों का निरपेक्ष मान ज्ञात करें अर्थात् यदि विचलनों में ऋण चिह्न लगा है तो उसे हटा दें अर्थात् |x₁ - a|, |x₂ - a|, |x₃ - a, ............... |x_n - a| ज्ञात करें ।
चरण 4. विचलनों के निरपेक्ष मानों का माध्य ज्ञात करें, यही माध्य 'a' के सापेक्ष माध्य विचलन है ।

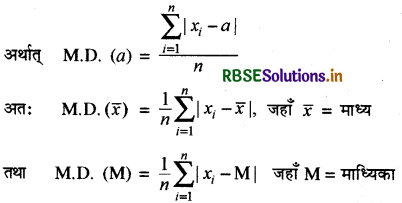
वर्गीकृत आँकड़ों के लिए माध्य विचलन (Mean deviation for grouped datas):
हम जानते हैं कि आँकड़ों को दो प्रकार से वर्गीकृत किया जाता
(a) असतत बारंबारता बंटन (Discrete frequency distribution)
(b) सतत बारंबारता बंटन (Continuous frequency distribution)
हम यहाँ पर दोनों प्रकार के आँकड़ों के लिए माध्य विचलन ज्ञात करने की विधियों की चर्चा करेंगे ।
(a) असतत बारंबारता बंटन (Discrete frequency distribution)
माना कि दिये गये आँकड़ों में n भिन्न प्रेक्षण x₁, x₂, x₃, ,.............। इनकी बारम्बारताएँ क्रमश: f₁, f₂, f₃, .......... f_n हैं। इन आँकड़ों को सारणीबद्ध रूप में निम्नलिखित प्रकार से व्यक्त किया जा सकता है, जिसे असतत बारंबारता बंटन कहते हैं ।

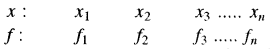
(i) माध्य के सापेक्ष माध्य विचलन - सबसे पहले हम दिये गये आँकड़ों का निम्नलिखित सूत्र के द्वारा माध्य (x̄) का मान ज्ञात करते हैं-

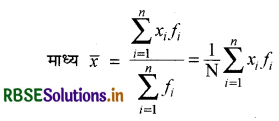
जहाँ \(\sum_{i=1}^n\)x_if_i प्रेक्षणों x_i का उनकी क्रमशः बारंबारता f_i से गुणनफलों का योग प्रकट करता है तथा N = \(\sum_{i=1}^n\)f_i बारंबारताओं के योग को प्रकट करता है ।
अब हम x; का माध्य से विचलन ज्ञात करते हैं और उन सभी का निरपेक्ष मान प्राप्त करते हैं अर्थात् सभी i = 1, 2, 3, ..............., n |x_i - x̄| का मान ज्ञात करते हैं ।

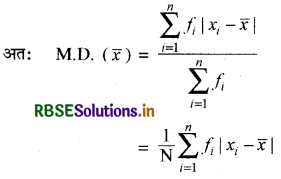
(ii) माध्यिका के सापेक्ष माध्य विचलन - इसके लिए हम असतत बारंबारता बंटन की माध्यिका ज्ञात करते हैं । इसके लिए दिए गए प्रेक्षणों को आरोही क्रम में लिखते हैं। इसके बाद संचयी बारंबारताएँ ज्ञात की जाती हैं तब उस प्रेक्षण का निर्धारण करते हैं जिसकी संचयी बारंबारता \(\frac{N}{2}\)के समान या इससे थोड़ी अधिक है । यहाँ बारंबारताओं का योग N से दर्शाया गया है। प्रेक्षणों का यह मान आँकड़ों के मध्य स्थित होता है इसलिए यह अपेक्षित माध्यिका है। माध्यिका ज्ञात करने के बाद हम माध्यिका से विचलनों के निरपेक्ष मानों का माध्य ज्ञात करते हैं। इस प्रकार माध्यिका से माध्य विचलन
M.D. (M) = \(\frac{1}{\mathrm{~N}} \sum_{i=1}^n\)f_i|x_i - M|

(b) सतत बारंबारता बंटन (Continuous frequency distribution):
एक सतत बारंबारता बंटन वह शृंखला होती है जिसमें आँकड़ों को विभिन्न बिना अन्तर वाले वर्गों में वर्गीकृत किया जाता है और उनकी क्रमशः बारंबारता लिखी जाती है ।
उदाहरण के लिए 100 छात्रों द्वारा प्राप्तांकों को सतत बारंबारता बंटन में निम्नलिखित प्रकार से व्यक्त किया गया है-

(i) माध्य के सापेक्ष माध्य विचलन- यहाँ पर प्रत्येक वर्ग की बारंबारता उसके मध्य - बिन्दु पर केन्द्रित होती है । मध्य बिन्दु को x से निरूपित करते हैं ।

माध्य के सापेक्ष माध्य विचलन ज्ञात करने की लघु विधि अर्थात् पद विचलन विधि (Step deviation method):
इस विधि में सबसे पहले x का मान निकालते हैं। इसके लिए हम आँकड़ों के मध्य या उसके बिल्कुल पास किसी प्रेक्षण को कल्पित माध्य मानते हैं । तब प्रेक्षणों या विभिन्न वर्गों के मध्य बिन्दुओं का इस कल्पित माध्य से विचलनों का मान निकालते हैं । यदि सभी विचलनों में कोई सार्व गुणनखण्ड होता है तो विचलनों के मान को सरल करने के लिए इन्हें इस सार्वगुणनखण्ड से भाग देते हैं । इन नये विचलनों को पद विचलन कहते हैं ।
माना कि 'a' कोई कल्पित माध्य है और h सार्वगुणनखण्ड है तब एक नया चर d_i = \(\frac{x_i-a}{h}\) लेते हैं।
तब x̄ माध्य का मान निम्न सूत्र से ज्ञात करते हैं-

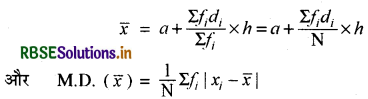
माध्य विचलन की परिसीमाएँ (Limitations of mean deviation):
(1) जब आँकड़ों में बहुत अधिक विचरण अर्थात् बिखराव हो, मध्यका के सापेक्ष प्राप्त माध्य विचलन पर निर्भर नहीं रहा जा सकता ।
(2) माध्य विचलन विचलनों के निरपेक्ष मानों पर निर्भर करता है इसलिए यह बीजगणितीय गणनाओं के योग्य नहीं होता है ।
(3) माध्य से विचलनों का योग (ऋण को छोड़कर) माध्यिका से विचलनों के योग से अधिक होता है । अतः माध्य के सापेक्ष माध्य विचलन वैज्ञानिक नहीं है । कई स्थितियों में यह संतोषजनक परिणाम नहीं देता है ।
अतः हमें प्रकीर्णन की एक अन्य माप की आवश्यकता है। मानक विचलन प्रकीर्णन की ऐसी ही एक माप है ।

प्रसरण और मानक विचलन (Variance and Standard Deviation):
माध्य विचलन ज्ञात करने के लिए केन्द्रीय प्रवृत्ति की माप के सापेक्ष विचलनों के निरपेक्ष मानों का योग किया जाता है। ऐसा माध्य विचलन को सार्थक बनाने के लिए किया जाता है । अन्यथा विचलनों का योग शून्य हो जाता है | इस गणितीय अशुद्धि अथवा अवहेलना को ठीक करने के लिए विचलन ज्ञात करने की एक और पद्धति काम में लाई जाती है। इस पद्धति के अन्तर्गत समान्तर माध्य निकालकर इससे सब चरों के मानों से विचलन निकाल लेते हैं और फिर सब विचलनों के वर्ग (square) निकाल लेते हैं। अन्त में इस वर्ग संख्याओं को जोड़कर उसका औसत ले लेते हैं तथा प्राप्त अंकों का वर्गमूल निकाल लेते हैं। इस प्रकार जो अंक प्राप्त होता है, मानक विचलन (Standard deviation) कहलाता है।
परिभाषाएँ -
मानक विचलन (Standard deviation) - " श्रेणी के विभिन्न चर मूल्यों के समान्तर माध्य से प्राप्त विचलन के वर्गों के समान्तर माध्य के वर्गमूल को मानक विचलन कहते हैं । "
मानक विचलन (σ) = \(\sqrt{\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}{n}}\)

मानक विचलन गुणांक ( Coefficient of Standard deviation): मानक विचलन एक निरपेक्ष मान है । दो श्रेणियों का तुलनात्मक अध्ययन करने के लिए मानक विचलन का सापेक्ष मान का प्रयोग करते हैं, जो मानक विचलन गुणांक (Coefficient of Standard Deviation) कहलाता है । इसका सूत्र निम्न प्रकार है-

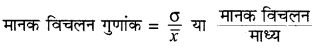
प्रसरण (Variance) - माध्य से लिए गए विचलनों के वर्गों के माध्य को प्रसरण कहते हैं । इसे σ² से निरूपित करते हैं ।
यदि x₁, x₂, x₃, .......... का समान्तर माध्यx हो तो प्रसरण

मानक विचलन (Standard Deviation):
किसी बंटन के विभिन्न पदों का उनके समान्तर माध्य से लिए गए विचलनों के वर्गों के समान्तर माध्य के धनात्मक वर्गमूल को उस बंटन का मानक विचलन कहते हैं और इसको σ से निरूपित करते हैं ।
अर्थात्
σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\)

एक असतत बारंबारता बंटन का मानक विचलन (Standard deviation of a discrete frequency distribution)
मान लीजिए कि दिया गया असतत बंटन निम्नलिखित है-

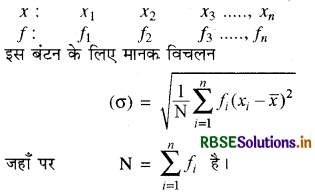
एक सतत बारंबारता बंटन का मानक विचलन (Standard deviation of a continuous frequency distribution):
दिए गए सतत बारंबारता बंटन के सभी वर्गों के मध्य मान लेकर उसे असतत बारंबारता बंटन में निरूपित कर सकते हैं । तब असतत बारंबारता बंटन के लिए अपनाई गई विधि द्वारा मानक विचलन ज्ञात किया जाता है
यदि एक वर्गों वाला बारंबारता बंटन जिसमें प्रत्येक अंतराल उसके मध्यमान x_i तथा बारंबारता f_i द्वारा परिभाषित किया गया है, तब मानक विचलन निम्नलिखित सूत्र द्वारा प्राप्त किया जाएगा-
σ = \(\sqrt{\frac{1}{\mathrm{~N}} \sum_{i=1}^n f_i\left(x_i-\bar{x}\right)^2}\)
यहाँ पर x, बंटन का माध्य है और N = \(\sum_{i=1}^n f_i\) है जो कि बारम्बारताओं का योग है ।
हम जानते हैं कि

प्रसरण व मानक विचलन ज्ञात करने के लिए लघु विधि (Shortcut method to find variance and standard deviation):
जब कभी - कभी एक बारंबारता बंटन के प्रेक्षणों x अथवा विभिन्न वर्गों के मध्यमान x के मान बहुत बड़े होते हैं तो माध्य तथा प्रसरण का मान ज्ञात करना कठिन हो जाता है तथा उसमें समय अधिक लगता है ऐसे बारंबारता बंटन, जिसमें वर्ग-अन्तराल समान हों, के लिए पद विचलन विधि द्वारा इस प्रक्रिया को सरल बनाया जा सकता है।

माना कि कल्पित माध्य ‘A’ है और मापक या पैमाने को \(\frac{1}{h}\) के गुना छोटा किया गया है (यहाँ h वर्ग अन्तराल है) । मान लीजिए कि पद विचलन या नया चर y_i है
अर्थात् y_i = \(\frac{x_i-\mathbf{A}}{h}\) या x_i = A + hy_i ..........(1)
हम जानते हैं कि x̄ = \(\frac{\sum_{i=1}^n f_i x_i}{\mathrm{~N}}\) ............(2)
समीकरण (1) से x_i को समीकरण (2) में रखने पर हमें प्राप्त होता है

बारंबारता बंटनों का विश्लेषण (Analysis of Frequency Distribution)
दो या दो से अधिक श्रेणियों के विक्षेपण की तुलना करने के लिए मानक विचलन गुणांक निकाला जाता है। जिसका मान सदैव एक से कम अर्थात् दशमलव भिन्न में ही आता है, जिससे अनुमान लगाने में असुविधा होती है । इसी कारण विचरण गुणांक का प्रयोग किया जाता है। मानक विचलन गुणांक को 100 से गुणा करने पर जो प्रतिशत आता है, उसे ही विचरण गुणांक (coefficient of variation) कहते हैं । वस्तुत: विचरण गुणांक मानक विचलन गुणांक का प्रतिशत रूप ही है । इसे निम्न सूत्र से ज्ञात किया जाता है
विचरण गुणांक (Coefficient of Variation)
C.V. = \(\frac{\sigma}{\bar{x}}\) × 100
जहाँ σ और x̄ क्रमशः आँकड़ों के मानक विचलन तथा माध्य है
दो श्रृंखलाओं में विचरण की तुलना के लिए हम प्रत्येक श्रृंखला का विचरण गुणांक ज्ञात करते हैं। दोनों में से बड़े विचरण गुणांक वाली शृंखला को अधिक विचरण या बिखराव वाली श्रृंखला कहते हैं। कम विचरण गुणांक वाली श्रृंखला को दूसरी से अधिक संगत कहते हैं ।

दो समान माध्य वाले बारंबारता बंटनों की तुलना (Comparison of two frequency distribution with same mean)
माना कि x̄₁ तथा σ₁ पहले बंटन के माध्यं तथा मानक विचलन हैं और तथा σ₂ दूसरे बंटन के माध्य और मानक विचलन हैं ।
पहले बंटन के लिए
C.V. = \(\frac{\sigma_1}{\bar{x}_1}\) × 100
दूसरे बंटन के लिए
C.V. = \(\frac{\sigma_1}{\bar{x}_1}\) × 100
दिया है
x̄₁ = x̄₂ = x̄ (मान लें )
इसलिए C. V. (पहला बंटन) = \(\frac{\sigma_1}{\bar{x}}\) × 100 .....(1)
और C.V. (दूसरा बंटन) = \(\frac{\sigma_2}{\bar{x}}\) × 100 ........(2)

समीकरण (1) तथा (2) से स्पष्ट है कि दोनों C.V. की तुलना σ₁ और σ₂ के आधार पर ही की जा सकती है अतः हम कह सकते हैं कि समान माध्य वाली शृंखलाओं में से अधिक मानक विचलन या प्रसरण वाली शृंखला को अधिक प्रक्षेपित कहा जाता है। साथ ही छोटी मानक विचलन या प्रसरण वाली श्रृंखला को दूसरी की अपेक्षा अधिक संगत कहा जाता है।

→ विक्षेपण (Dispersion): किसी श्रेणी के पदों का माध्य से बिखराव विक्षेपण कहलाता है। किसी श्रेणी का विक्षेपण उसके विभिन्न पदों के विचरण (Variation) या अन्तर का माप है । विक्षेपण के माप दो प्रकार के होते हैं-
(i) निरपेक्ष माप (Absolute measure)
(ii) सापेक्ष माप (Relative measure)

अर्थात् आँकड़ों में प्रकीर्णन या विक्षेपण का माप प्रेक्षणों व वहाँ प्रयुक्त केन्द्रीय प्रवृत्ति की माप के आधार पर किया जाता है । प्रकीर्णन के निम्नलिखित माप हैं-
(i) परिसर (Range)
(ii) चतुर्थक विचलन
(iii) माध्य विचलन
(iv) मानक विचलन

→ परास या विस्तार (Range): श्रेणी में चर के उच्चतम मान (H) और निम्नतम मान (L) के अन्तर को परास (R) या विस्तार कहते हैं । यदि चर सतत् श्रेणी के रूप में दिए गए हों, तो सबसे बड़े वर्ग की उच्च सीमा तथा सबसे छोटे वर्ग की निम्न सीमा का अन्तर ही परास कहलाता है ।
परिसर विक्षेपण का सबसे सरल माप है।
एक श्रृंखला का परिसर = अधिकतम मान - न्यूनतम मान
= H - L

→ माध्य विचलन (Mean Deviation): किसी भी श्रेणी में चर के विभिन्न मानों का, उसके सांख्यिकीय माध्य (स.मा., माध्यिका एवं बहुलक) से लिए गए विचलनों के निरपेक्ष मानों का समान्तर माध्य उसका माध्य विचलन कहलाता है ।

→ अवर्गीकृत आँकड़ों का माध्य विचलन-
M.D. (x̄) = \(\frac{\sum\left|\left(x_i-\bar{x}\right)\right|}{n}\)
M.D. (M) = \(\frac{\sum\left|\left(x_i-\mathrm{M}\right)\right|}{n}\)
जहाँ x̄ = चरों का माध्य है और M = चरों की माध्यिका है और n = चरों की संख्या है।

→ वर्गीकृत आँकड़ों का माध्य विचलन-
M.D. (x̄) = \(\frac{\sum f_i\left|\left(x_i-\bar{x}\right)\right|}{\mathrm{N}}\)
M.D. (M) = \(\frac{\Sigma f_i\left|\left(x_i-\mathrm{M}\right)\right|}{\mathrm{N}}\)
जहाँ पर N = Σf_i

→ असतत् बारंबारता बंटन का प्रसरण तथा मानक विचलन-
σ² = \(\frac{1}{\mathrm{~N}} \Sigma f_i\left(x_i-\bar{x}\right)^2\)
σ = \(\sqrt{\frac{1}{\mathrm{~N}} \sum f_i\left(x_i-\bar{x}\right)^2}\)

→ सतत् बारंबारता बंटन का प्रसरण तथा मानक विचलन-
σ² = \(\frac{1}{\mathrm{~N}} \Sigma f_i\left(x_i-\bar{x}\right)^2\)
σ = \(\frac{1}{\mathrm{~N}} \sqrt{\mathrm{N} \Sigma f_i x_i^2-\left(\Sigma f_i x_i\right)^2}\)

→ प्रसरण और मानक विचलन ज्ञात करने की लघु विधि-

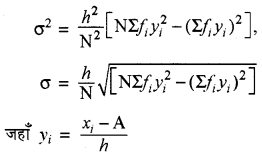
→ विचरण गुणांक C.V. = \(\frac{\sigma}{\bar{x}}\) × 100, x̄ ≠ 0

→ समान माध्य वाली श्रृंखलाओं में छोटी मानक विचलन वाली श्रृंखला अधिक संगत या कम विचरण वाली होती है।

→ यदि प्रत्येक प्रेक्षण को K, से गुणा किया जाये, तो नये बने प्रेक्षणों का प्रसरण, पूर्व प्रसरण का K² गुना हो जाता है ।

→ प्रेक्षणों के किसी समूह में प्रत्येक प्रेक्षण में कोई एक संख्या जोड़ने अथवा घटाने पर प्रसरण अपरिवर्तित रहता है ।