RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 6 Application of Derivatives Ex 6.2

Question 1.
Show that the function given by f(x) = 3x + 17 is increasing on R.
Answer:
Given,
f(x) = 3x + 17
Let x₁, x₂ ∈ R such that x₁ < x₂
3x₁ < 3x₂
3x₁ + 17 < 3x₂ + 17
f(x₁) < f(x₂)
∴ x₁ < x₂
f(x₁) < f(x₂)
Thus, f(x) = 3x + 17, is strictly increasing at R.
Hence Proved.

Question 2.
Show that the function given by .f(x) = e^2x is increasing on R.
Answer:
Given, f(x) = e^2x
∴ f'(x) = 2e^2x
For ∀ x ∈ R, f'(x) > 0
Since 2 > 0, e^2x > 0
Thus, function f, is strictly increasing at R.
Hence Proved.

Question 3.
Show that the function given by f(x) = sin x is
(a) increasing in \(\left(0, \frac{\pi}{2}\right)\)
(b) decreasing in \(\left(0, \frac{\pi}{2}\right)\)
(c) neither increasing nor decreasing in (0, π)
Answer:
Given, f(x) = sin x
⇒ f’(x) = cos x

(a) For interval \(\left(0, \frac{\pi}{2}\right)\)
f’(x) = cos x > 0
∴ In x ∈ \(\left(0, \frac{\pi}{2}\right)\) f’(x) is positive.
Thus, f is strictly increasing in interval \(\left(0, \frac{\pi}{2}\right)\).
Hence Proved.

(b) In interval \(\left(\frac{\pi}{2}, \pi\right)\)
f’(x) = cos x < 0 ⇒ f’(x) < 0
∴ In x ∈ \(\left(\frac{\pi}{2}, \pi\right)\), f’(x) < 0
Thus, function is strictly decreasing in interval \(\left(\frac{\pi}{2}, \pi\right)\).
Hence Proved.

(c) In interval (0, π),
f’(x) is not continuous +ve or -ve because in \(\left(0, \frac{\pi}{2}\right)\)
f'(x) positive f’(x) > 0 and \(\left(\frac{\pi}{2}, \pi\right)\)
f’(x) negative {f’(x) < 0}.
Thus, f, is neither increasing nor decreasing in interval (0, π).
Hence Proved.

Question 4.
Find the intervals in which the function f given by f(x) = 2x² - 3x is:
(a) increasing (b) decreasing
Answer:
Here f(x) = 2x² - 3x
∴ f’(x) = 4x - 3
f'(x) = 0, then 4x - 3 = 0
∴ x = 3/4
Thus, point x = 3/4 divides real number line into two disjoint intervals \(\left(-\infty, \frac{3}{4}\right)\) and \(\left(-\infty, \frac{3}{4}\right)\).

(a) In interval \(\left(\frac{3}{4}, \infty\right)\), f’(x) = positive
For x = 1 f’(x) = 4 - 3 = 1 > 0
∴ f is stricly increasing.
Thus, function is strictly increasing in interval \(\left(\frac{3}{4}, \infty\right)\).

(b) In interval \(\left(-\infty, \frac{3}{4}\right)\), f’(x) negative
For x = - 1, f’(x) = - 4 - 3 = - 7 < 0
∴ f is strictly decreasing function.
Thus, function is strictly decreasing in interval \(\left(-\infty, \frac{3}{4}\right)\)

Question 5.
Find the intervals in which the function f given by f(x) = 2x³ - 3x² - 36x + 7 is
(a) Increasing
(b) decreasing
Answer:
Given, f(x) = 2x³ - 3x² - 36x + 7
⇒ f’(x) = 6x² - 6x - 36
f’(x) = 0
⇒ 6x² - 6x - 36 = 0
⇒ 6(x² - x - 6) = 0
⇒ 6(x - 3) (x + 2) = 0
Either x - 3 = 0 or x + 2 = 0
⇒ x = 3 or x = - 2
Points x = - 2, x = 3 divide real number line into three disjoint intervals namely (- ∞, - 2), (- 2, 3) and (3, ∞).

(a) For interval (- ∞, - 2)
f’(x) = 6x² - 6x - 36 > 0
Since, at x = - 3
f’(x) = 6(- 3)² - 6(- 3) - 36
= 6 × 9 + 6 × 3 - 36
= 54 + 18 - 36
= 36 > 0
Similarly, we can prove f(x) > 0 for n ∈ (- ∞, - 2).
Thus, in (- ∞ - 2) function is strictly increasing i.e., for x ∈ (- ∞, - 2) function is strictly increasing.

(b) For interval (- 2, 3)
f’(x) = 6x² - 6x - 36 < 0
Since, at x = 1,
f’(x) = 6(1)² - 6 × 1 - 36
= 6 - 6 - 36
= - 36 < 0
At x = 0, f’(x) = 6(0)² - 6 × 0 - 36
= - 36 < 0
Similarly, we can prove f’(x) < 0.
For x ∈ (- 2, 3) function is strictly decreasing.

(c) For interval (3, ∞)
f’(x) = 6x² - 6x - 36 > 0
Since, at x = 4,
f’(x) = 6 × (4)² - 6 × 4 - 36
= 96 - 24 - 36
= 96 - 60
= 36 > 0
At x = 5,
f’(x) = 6(5)² - 6 × 5 - 36
= 6 × 25 - 30 - 36
= 150 - 30 - 36 = 84 > 0
Similarly, we can show for other points that f’(x) > 0. Thus, for x ∈ (3, ∞), function is strictly increasing hence, function f is strictly increasing in interval:
(- ∞ - 2) ∪ (3, ∞) f{f'(x) > 0}
In interval (- 2, 3), function strictly decreasing f{f'(x) < 0}.

Question 6.
Find the intervals in which the following functions are strictly increasing or decreasing:
(a) f(x) = x² + 2x + 5
Answer:
Given, f(x) = x² + 2x + 5
⇒ f’(x) = 2x + 2
f’(x) = 0 ⇒ 2x + 2 = 0
⇒ 2(x + 1) = 0 ⇒ x + 1 = 0 ⇒ x = - 1
Point x = - 1 divides real number line into two disjoint intervals namely (- ∞, - 1) and (- 1, ∞).

(i) In interval (- ∞, - 1)
f’(x) = 2(x + 1) < 0
Since, in x ∈ (- ∞, - 1), x < 0
For x = - 2
f’(x) = 2(- 2 + 1) = 2(- 1) = - 2 < 0
For x = - 3
f’(x) = 2(- 3 + 1) = 2(- 2) = - 4 < 0 Similarly, it can be shown for other points also. Thus, for x ∈ (- ∞, - 1), function is strictly decreasing.

(ii) For interval (- 1, ∞), f’(x) = 2(x + 1) > 0
Since x > - 1
For x = 0
f’(x) = 2(0 + 1) - 2 × 1 = 2 > 0
For x = 1
f’(x) = 2(1 + 1) = 2 × 2 = 4 > 0
Similarly, it can be shown for other points also.
Thus, for x ∈ (- 1, ∞), function f is strictly increasing.

(b) f(x) = 10 - 6x - 2x²
Answer:
Given, f(x) = 10 - 6x - 2x²
⇒ f’(x) = - 6 - 4x = - 2(3 + 2x)
f’(x) = 0 ⇒ - 2(3 + 2x) = 0
⇒ 3 + 2x = 0 ⇒ x = -\(\frac{3}{2}\)
Point x = -\(\frac{3}{2}\) divides real number line into two disjoints intervals namely (- ∞, - \(\frac{3}{2}\)) and (- \(\frac{3}{2}\), ∞).

(i) For interval \(\left(-\infty,-\frac{3}{2}\right)\)
f’(x) = - 2(3 + 2x) > 0
For x = - 2
f’(x) = - 2{3 + 2(- 2)) = - 2(3 - 4)
= - 2(- 1) = 2 > 0
For x = - 3
f’(x) = - 2{3 + 2(- 3)} = - 2(3 - 6)
= - 2(- 3) = 6 > 0
Similarly, it can be shown for other points also that f’(x) > 0
Thus, for x ∈ (- ∞, -\(\frac{3}{2}\)), function f is strictly increasing.

(ii) For interval \(\left(-\frac{3}{2}, \infty\right)\)
f’(x) = - 2(3 + 2x) < 0
For x = - 1,
f(x) = - 2{3 + 2(- 1)1 = - 2(3 - 2)
= - 2 × 1 = - 2 < 0
For x = 0
f’(x) = - 2(3 + 2 × 0)
= - 2 × 3 = - 6 < 0
For x = 1,
f’(x) = - 2(3 + 2 × 1) = - 2(3 + 2)
= - 2 × 5 = - 10 < 0
Similarly, it can be shown for other points also.
Thus for x ∈ \(\left(-\frac{3}{2}, \infty\right)\) function f is strictly decreasing.

(c) f(x) = - 2x³ - 9x² - 12x + 1
Answer:
Given, f(x) = - 2x³ - 9x² - 12x + 1
⇒ f’(x) = - 6x² - 18x - 12 = - 6(x² + 3x + 2)
f(x) = 0 ⇒ - 6(x² + 3x + 2) = 0
Either x + 2 = 0 or x + 1 = 0
= x = - 2 or x = - 1
Points x = - 2 and x = - 1 divide real number line into three intervals namely (- ∞, - 2), (- 2, - 1) and (- 1, ∞).

(i) For interval (- ∞, - 2)
f’(x) = - 6(x² + 3x + 2) < 0
For x = - 3
f’(x) = 6{(- 3)² + 3(- 3) + 21
= - 6(9 - 9 + 2) = - 12 < 0
For x = - 4
f’(x) = - 6{(- 4)² + 3(- 4) + 2}
= - 6(16 - 12 + 2) - 36 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- ∞, - 2) function is strictly decreasing.

(ii) For interval (- 2, - 1)
f’(x) = - 6(x² + 3x + 2) > 0
For x = - 1.5
f’(x) = - 6{(- 1.5)² + 3(- 1.5) + 2)}
= - 6(2.25 - 4.5 + 2)
= + 1.50 > 0
Similarly, by taking another point we can show that f’(x) > 0.
Thus, f for x ∈ (- 2, - 1) function is strictly increasing.

(iii) For interval (- 1, ∞)
f’(x) = - 6(x² + 3x + 2) < 0
For x = 0
f’(x) = - 6(0² + 3 × 0 + 2)
= - 6 × 2 = - 12 < 0
For x = 1
f’(x) = - 6{(1)² + 3 × 1 + 2}
= - 6(1 + 3 + 2) = - 36 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- 1, ∞) function f is strictly decreasing.
Thus, by (i) and (iii) we can say that function is strictly decreasing in (- ∞, - 2) ∪ (- 1, ∞).

(d) f(x) = 6 - 9x - x²
Answer:
Given, f(x) = 6 - 9x - x²
⇒ f’(x) = - 9 - 2x
f’(x) = 0 ⇒ - 9 - 2x = 0
⇒ - 2x = 9 ⇒ x = -\(\frac{9}{2}\)
Point x = -\(\frac{9}{2}\) divides real number line into two disjoints intervals namely \(\left(-\infty,-\frac{9}{2}\right)\) and \(\left(-\frac{9}{2}, \infty\right)\).

(i) For \(\left(-\infty,-\frac{9}{2}\right)\)
f’(x) = - 9 - 2x > 0
For x = - 5
f’(x) = - 9 - 2(- 5) - 9 + 10 = 1 > 0
For x = - 6
f’(x) = - 9 - 2(- 6) = - 9 + 123 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, for x ∈ \(\left(-\infty,-\frac{9}{2}\right)\), function f is strictly increasing.

(ii) For interval \(\left(-\frac{9}{2}, \infty\right)\)
f’(x) = - 9 - 2x < 0
For x = - 4
f’(x) = - 9 - 2(- 4) - 9 + 8 - 1 < 0
For x = - 3
f’(x) = - 9 - 2(- 3) = - 9 + 6 = - 3 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ \(\left(-\frac{9}{2}, \infty\right)\) function f is strictly decreasing.

(e) f(x) = (x + 1)³ (x - 3)³
Answer:
Given, f(x) = (x + 1)³ (x - 3)³
⇒ f’(x) = (x + 1)³.\(\frac{d}{d x}\)f(x - 3)³ +(x - 3)³ \(\frac{d}{d x}\) (x + 1)³
⇒ f’(x) = (x + 1)³.3(x - 3)³ + (x - 3)³.3(x + 1)²
⇒ f’(x) = 3(x + 1)² (x - 3)² [(x + 1 + x - 3)]
⇒ f’(x) = 3(x + 1)² (x - 3)² (2x - 2)
⇒ f’(x) = 3(x + 1)² (x - 3)² 2(x —1)
⇒ f’(x) = 6(x -1) (x + 1)² (x - 3)²
f’(x) = 0
⇒ 6(x - 1) (x + 1)² (x - 3)² = 0
⇒ x - 1 = 0 or (x + 1)² = 0 or (x - 3)² = 0
⇒ x = 1 or x = - 1 or x = 3
Points x = - 1, x = 1 and x = 3 divide real number line into four disjoint intervals namely (- ∞, - 1), (- 1, 1), (1, 3) and (3, ∞).

(i) For interval (- ∞ , - 1)
f’(x) = 6(x - 1) (x + 1)² (x - 3)² < 0
For x -2
f’(x) = 6(- 2 - 1) (- 2 + 1)² (- 2 - 3)²
⇒ f’(x) = 6(- 3) (- 1)² (- 5)²
⇒ f’(x) = - 18 × 1 × 25 = - 450 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- ∞, - 1), function f is strictly decreasing.

(ii) For interval (- 1, 1)
f’(x) = 6(x - 1) (x + 1)² (x - 3)² < 0
For x = 0
f’(x) = 6(0 - 1) (0 + 1)² (0 - 3)²
= 6 × (- 1) × 1 × 9 = - 54 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (-1, 1), function f is strictly decreasing.

(iii) For interval (1, 3)
f’(x) = 6(x - 1) (x + 1)² (x - 3)² > 0
For x = 2
f’(x) = 6(2 - 1) (2 + 1)² (2 - 3)²
= 6 × 1 × 9 × 1 = 54 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, for x ∈ (1, 3), function f is strictly decreasing.

(iv) For interval (3, ∞)
f’(x) = 6(x - 1) (x + 1)² (x - 3)² > 0
For x = 4
f’(x) = 6(4 - 1) (4 + 1)² (4 - 3)²
= 6 × 3 × 25 × 1
= 450 > 0
Similarly, by taking another points we can show that
f’(x) > 0.
Thus, for x ∈ (3, ∞), function f is strictly increasing.

Question 7.
Show that y = log(1 + x) - 2. \(\frac{2 x}{2+x}\), x > - 1 is an increasing function of x throughout its domain.
Answer:
Let y = f(x)

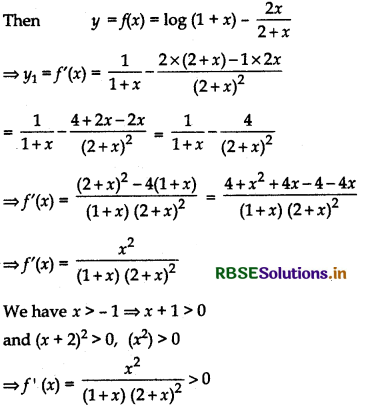
Thus, function is strictly increasing in its domain.
Hence Proved.

Question 8.
Find the values of x for which y = [x(x - 2)]² is an increasing function.
Answer:
Let y = f(x)
= y = f(x) = [x(x - 2)]²
y = f(x) = (x² - 2x)²
y = f(x) = x⁴ - 4x³ + 4x²
= \(\frac{d y}{d x}\) = f’(x) = 4x³ - 12x² + 8x
f’(x) = 4x(x² - 3x + 2)
f’(x) = 0
4x(x² - 3x + 2) = 0
4x(x - 2) (x - 1) = 0
x = 0 or x = 2 or x = 1
Point x = 0, x = 1 and x = 2 divide real number line into four disjoints intervals namely (- ∞, 0), (0, 1), (1, 2) and (2, ∞).

(i) For interval (- ∞, 0)
f’(x) = 4x³ - 12x² + 8x
= 4x(x - 2) (x - 1) < 0
For x = - 1
f’(x) = 4(- 1)³ - 12(- 1)² + 8(- 1)
= - 4 - 12 - 8 = - 24 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, function is strictly decreasing for x ∈ (- ∞, 0).

(ii) For interval (0, 1)
f’(x) = 4x(x - 2) (x - 1) > 0
Fo x = \(\frac{1}{2}\)
f(x) = 4 × \(\frac{1}{2}\left(\frac{1}{2}-2\right)\left(\frac{1}{2}-1\right)\)
= 2\(\left(-\frac{3}{2}\right)\left(-\frac{1}{2}\right)=\frac{3}{2}\) > 0
Similarly, by taking another points we can show that f’(x) >0.
Thus, function is strictly increasing for x ∈ (0, 1).

(iii) For interval (1, 2)
f’(x) = 4x(x - 1) (x - 2) < 0
For x = \(\frac{3}{2}\)
f’(x) = 4 \(\times \frac{3}{2}\left(\frac{3}{2}-1\right)\left(\frac{3}{2}-2\right)\)
= \(6\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)=-\frac{3}{2}\) < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, function is strictly decreasing for x ∈ (1, 2).

(iv) For interval (2, ∞)
f’(x) = 4x(x - 1) (x - 2) > 0
For x = 3
f’(x) = 4 × 3(3 - 1) (3 - 2)
= 4 × 3 × 2 × 1 = 24 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, function is strictly increasing for x ∈ (2, ∞).
Hence, function is increasing in x ∈ (0, 1) ∪ (2, ∞).

Question 9.
Prove that y = \(\frac{4 \sin \theta}{(2+\cos \theta)}\) - θ is an increasing function of θ in \(\left(0, \frac{\pi}{2}\right)\).
Answer:
Let y = f(θ)

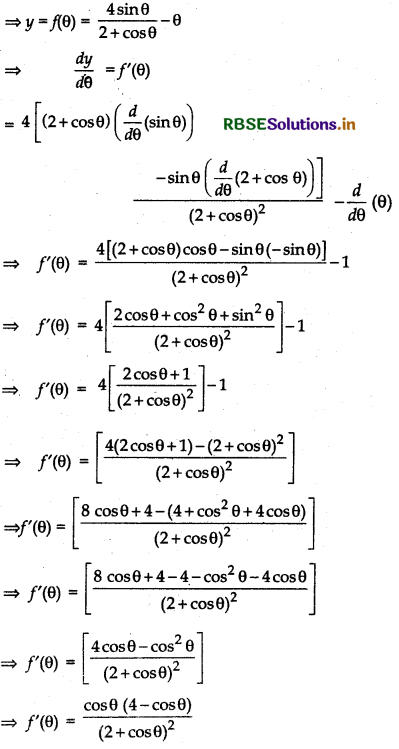
In interval \(\left[0, \frac{\pi}{2}\right]\), cos θ > 0 and 4 - cos θ > 0, since - 1 ≤ cos θ ≤ 1 and (2 + cos θ)² > 0.
∴ f’(θ) > 0
Hence, in interval [0, π/2], function f is strictly increasing.
Hence Proved.

Question 10.
Prove that the logarithmic function is increasing on (0, ∞).
Answer:
Let f(x) = log x, x > 0
⇒ f’(x) = \(\frac{1}{x}\) > 0, for x > 0
∴ f’(x) > 0
Thus, logarithmic function is strictly increasing in (0, ∞).
Hence Proved.

Question 11.
Prove that the function f given by
f(x) = x² - x + 1
is neither strictly increasing nor decreasing on (- 1, 1).
Answer:
Given, f(x) = x² - x + 1
⇒ f’(x) = 2x - 1
f’(x) = 0 ⇒ 2x - 10
⇒ 2x = 1 ⇒ x = 1/2
Point x = \(\frac{1}{2}\) divides line into two disjoints intervals namely \(\left(-1, \frac{1}{2}\right)\) and \(\left(\frac{1}{2}, 1\right)\).

(i) For interval \(\left(-1, \frac{1}{2}\right)\)
f’(x) = 2x - 1 < 0
For x = 0
f’(x) = 2 × 0 - 1 = - 1 < 0
Similarly, we can prove for other points f’(x) < 0. Thus,, for x ∈ \(\left(-1 ; \frac{1}{2}\right)\) function is strictly decreasing. (ii) For interval \(\left(\frac{1}{2}, 1\right)\) f’(x) = 2x - 1 > 0
For x = \(\frac{3}{4}\)
f'(x) = 2 × \(\frac{3}{4}\) - 1 = \(\frac{3}{2}\) - 1 = \(\frac{1}{2}\) > 0
Similarly, we can prove for other points f’(x) > 0.
Thus, function is strictly increasing for x ∈ \(\left(\frac{1}{2}, 1\right)\).
Hence, function is decreasing in x ∈ \(\left(-1, \frac{1}{2}\right)\) and increasing in \(\left(\frac{1}{2}, 1\right)\).
Hence, function is neither increasing nor decreasing in interval (- 1, 1).

Question 12.
Which of the following functions are decreasing in \(\left(0, \frac{\pi}{2}\right)\)?
(A) cos x
Answer:
Let f(x) = cos x
f’(x) = - sin x
In interval \(\left(0, \frac{\pi}{2}\right)\), sin x > 0 ⇒ - sin x < 0
⇒ f’(x) < 0 Thus, function f(x) = cos x, is strictly decreasing in \(\left(0, \frac{\pi}{2}\right)\).

(B) cos 2x
Answer:
Let f(x) = cos 2x
⇒ f’(x) = - 2 sin 2x
In interval \(\left(0, \frac{\pi}{2}\right)\), sin 2x > 0 (0 < 2x < π)
⇒ - sin 2x < 0 ⇒ f'(x) < 0
Thus, in interval \(\left(0, \frac{\pi}{2}\right)\) cos 2x is strictly decreasing.

(C) cos 3x
Answer:
Let f(x) = cos 3x
⇒ f’(x) = - 3 sin 3x
When x ∈ \(\left(0, \frac{\pi}{2}\right)\)
⇒ 0 < x < \(\frac{\pi}{2}\)
⇒ 0 < 3x < \(\frac{\pi}{2}\)
⇒ sin 3x may be + ve or - ve.
⇒ f’(x) = - 3 sin 3x is +ve and -ve.
Thus, in interval \(\left(0, \frac{\pi}{2}\right)\) function f is neither increasing nor decreasing.

(D) tan x
Answer:
Let f(x) = tan x
⇒ f’(x) = sec²x
In interval \(\left(0, \frac{\pi}{2}\right)\), sec x > 0
⇒ sec² x > 0 ⇒ f’ (x) > 0
Thus, in interval \(\left(0, \frac{\pi}{2}\right)\), tan x is strictly increasing.

Question 13.
On 1rhich of the following intervals is the function f given by f(x) = x¹⁰⁰ + sin x - 1 decreasing?
(A) (0, 1)
(B) \(\left(\frac{\pi}{2}, \pi\right)\)
(C) \(\left(0, \frac{\pi}{2}\right)\)
(D) none of these
Answer:
Given, f(x) = x¹⁰⁰ + sin x - 1
f’(x) = 100x⁹⁹ + cos x

(A) For interval (0, 1), 0 < x < 1
⇒ 0 < 100x⁹⁹ < 100 and cos x > 0
∴ 100x⁹⁹ + cos x > 0 ⇒ f’(x) > 0
∴ Function f(x) = x¹⁰⁰ + sin x - 1 is increasing in interval (0, 1).

(B) For interval \(\left(\frac{\pi}{2}, \pi\right)\)
x ∈ \(\left(\frac{\pi}{2}, \pi\right)\)
⇒ x ∈ \(\left(\frac{\pi}{2}, \pi\right)\)
⇒ x⁹⁹ > 1
⇒ 100x⁹⁹ > 100
∴ \(\left(\frac{\pi}{2}, \pi\right)\)
∴ - 1 < cos x < 0 ⇒ 0 > cos x > - 1
∴ From equation (1) and (2)
100x⁹⁹ + cos x > 100 - 1 = 99
100x⁹⁹ + cos x > 0
⇒ f’(x) >0 (∴ f’(x) = 100x⁹⁹ + cos x)
∴ In \(\left(0, \frac{\pi}{2}\right)\), f(x) is increasing.

(C) For interval \(\left(0, \frac{\pi}{2}\right)\)
f’(x) = 100x⁹⁹ + cos x > 0
Since cos x > 0 and 100x⁹⁹ > 0
⇒ f’(x) > 0
∴ In interval \(\left(0, \frac{\pi}{2}\right)\) function j is increasing.
We see that function f is increasing for all intervals.
Hence, (D) is correct.

Question 14.
For what values of a the function f given by f(x) = x² + ax + 1 is increasing on (1, 2)?
Answer:
Given, f(x) = x² + ax + 1
⇒ f’(x) = 2x + a
x ∈ (1,2)
⇒ 1 < x < 2 ⇒ 2 < 2x < 4
⇒ 2 + a < 2x + a < 4 + a ⇒ 2 + a > 0
∴ a > - 2.
Thus, least value of a is - 2
For a = -2
f’(x) = 2x - 2 = 2(x - 1) > 0 [∴ 1 < x < 2]

Question 15.
Let be any interval disjoint from (-1, 1). Prove that the function f given by f(x) = x + \(\frac{1}{x}\) is increasing on I.
Answer:
Given, f(x) = x + \(\frac{1}{x}\)
⇒ f(x) = 1 - \(\frac{1}{x^{2}}\) = \(\frac{x^{2}-1}{x^{2}}\)
Given, I is such interval which is disjoint from (- 1, 1)
x < - 1 and x > 1
f’(x) > 0
If \(\frac{x^{2}-1}{x^{2}}\) > 0 ⇒ x² > 1
⇒ x < - 1 and x > 1
∴ In this interval f’(x) > 0.
Thus, function f is strictly increasing where x < -1, x > 1.
Hence, f(x), is strictly increasing in I.
Hence Proved.

Question 16.
Prove that the function f given by f(x) = log sin x, increasing on \(\left(0, \frac{\pi}{2}\right)\) and decreasing on \(\left(\frac{\pi}{2}, \pi\right)\).
Answer:
Given, f(x) = log sin x

Question 17.
Prove that the function f given by f(x) = log | cos x | is decreasing on \(\left(0, \frac{\pi}{2}\right)\) and increasing on \(\left(\frac{3 \pi}{2}, 2 \pi\right)\).
Answer:
Given, f(x) = log cos x

Question 18.
Prove that the function given by f(x) = x³ - 3x² + 3x -100 is increasing in R.
Answer:
f(x) = x³ - 3x² + 3x - 100
f’(x) = 3x² - 6x + 3
f’(x) = 3(x² - 2x + 1)
f’(x) = 3(x - 1)² > 0
f’(x) > 0 {∵ (x - 1)² > 0 ∀ x ∈ R)
Hence, in function, R is strictly increasing.
Hence Proved.

Question 19.
The interval in which y = x²e is increasing is:
(A) (- ∞, ∞)
(B) (- 2, 0)
(C) (2, ∞)
(D) (0, 2)
Answer:
Let y = f(x) = x²e^-x
⇒ f’(x) = \(\frac{d y}{d x}\) = 2xe^-x + x² (- 1)e^-x = 2xe^{- x} - x²e^-x
⇒ f’(x) = e^-x.x (2 - x) = - xe^-x (x - 2)
If function f is increasing, then
f’(x) > 0 ⇒ - x e^-x (x - 2) > 0

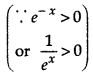
⇒ - x(x - 2) > 0
⇒ x(x - 2) < 0 ⇒ x ∈ (0, 2) ⇒ f’(x) > 0
∴ Function f is increasing in interval (0, 2).
Thus, (D) is correct.